Related Resources: heat transfer
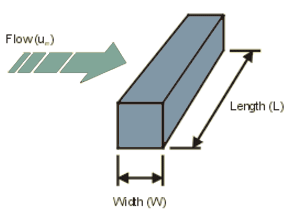
Square Rod Forced Air Convection Isothermal Equation and Calculator
Heat Transfer Engineering
Thermodynamics
Engineering Physics
Isothermal Square Rod Forced Air Convection Equation and Calculator
Average convection heat transfer coefficient and heat convected from an isothermal (constant temperature) flat plate at a specified temperature in free stream flow.
ALL calculators require a Premium Membership
Preview: Isothermal Square Rod Forced Air Convection Calculator
Calculations is based on Nusselt number correlations. The heat flow (q) from the rod is calculated as:
q = h · A · (Tp - Ta )
h = Nu · k / W
The Nusselt number is calculated as:
Nu = C Ren Pr0.33
C and n are 0.102 and 0.675 respectively.
Re = u m · W / v
Pr = v /a
Fluid properties at the film temperature Tf defined as follows:
Tf = (Tr + Ta ) / 2
Correlations are valid for Reynolds numbers in the range of 5000 and 100000 and Prandtl numbers in the range of 0.6 and 50. These calculations are not suitable for low Prandtl fluids like liquid metals and high Prandtl fluids like heavy oils or silicons.
Where:
q = Heat Dissipated (W)
k = Thermal Conductivity of Fluid (W/m - °C)
h = Heat transfer coefficient (W/m2 - °C)
W = Rod width (m)
L = Rod length (m)
Tr = Rod temperature °C
Ta = Ambient fluid temperature °C
Tf = Film temperature °C
h = Average heat transfer coefficient (W/m2 - °C)
Nu = Nusselt Number
u m = Fluid/Flow Velocity (m/s)
Re = Reynolds number
Pr = Prandtl number
Re = Fluid velocity x Length / kinematic viscosity
v = Kinematic viscosity (m2/s)
cp = Specific Heat capacity (J/(kg·K))
v = Dynamic Viscosity (kg/m-s)
a = Thermal Diffusivity (m2/s)
The above correlations are valid for Prandlt numbers in the range of 0.6 and 50 and are not suitable for low Prandtl fluids like liquid metals and high Prandtl fluids like heavy oils or silicons.
References
Holman, J.P., Heat Transfer , 7th ed., McGraw Hill Book Company, New York, 1990. p 281 - 306