Volumes of Solids Equation and Calculation Menu
Mathematics Menu
Engineering Basic Menu
Engineering Analysis Menu
- The following are to links of Volumes of Solids Equations, calculators, articles and other useful data.
- Should you find any errors omissions broken links, please let us know - Feedback
** Search this PAGE ONLY, click on Maginifying Glass **
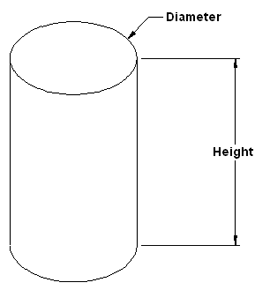 |
Concrete Column Volume Calculator Volume of concrete to fill the width and height of a column. |
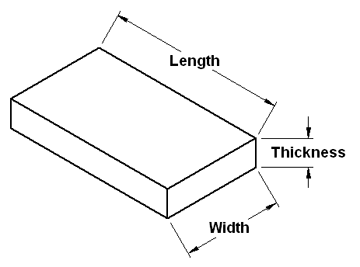 |
Concrete Slab Volume Calculator Concrete volume to fill the width, height and depth given. |
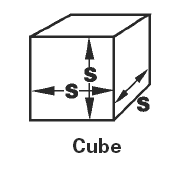 |
Cube Volume Equations and Calculator Volume Equation and Calculator of Cube |
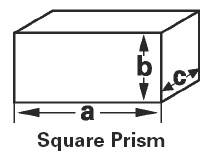 |
Square Prism Volume Equations and Calculator Volume Equation and Calculator of Prism |
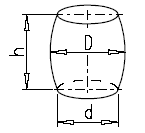 |
Barrel Volume Equations and Calculator Volume Equation and Calculator of Barrel |
 |
Cylinder Volume and Surface Area Equation and Calculator Volume Equation and Calculator of Cylinder |
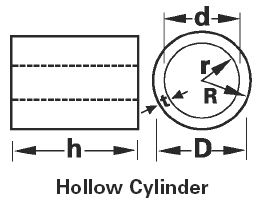 |
Hollow Cylinder Volume Equation and Calculator Volume Equation and Calculator of Hollow Cylinder |
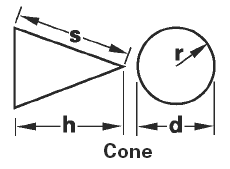 |
Cone Volume and Area Equation and Calculator Volume Equation and Calculator of Cone |
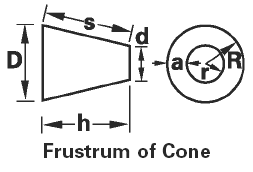 |
Frustrum of Cone Volume and Area Equation and Calculator Volume Equation and Calculator of Cone Frustrum |
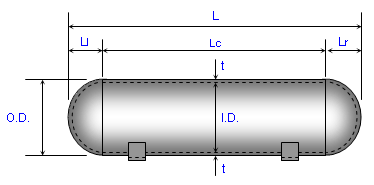 |
Propane Tank Volume Calculator Determine the volume of a cylindrical tank with spherical ends. |
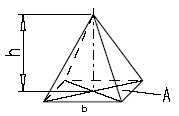 |
Pyramid Volume and Area Equation and Calculator Volume Equation and Calculator of Pyramid |
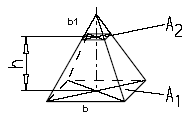 |
Pyramid Frustrum Volume and Area Equation and Calculator Volume Equation and Calculator of Frustrum Pyramid |
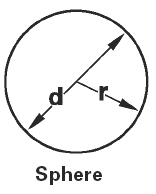 |
Sphere Volume and Area Equation and Calculator Volume Equation and Calculator of Sphere |
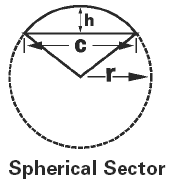 |
Spherical Sector Area, Volume Equation and Calculator Volume Equation and Calculator of Sector of Sphere |
 |
Spherical Segment Volume and Area Equation and Calculator Volume Equation and Calculator of Spherical Sector |
 |
Spherical Zone Volume and Area Equation and Calculator Volume Equation and Calculator of Spherical Zone |
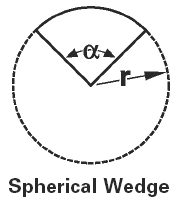 |
Spherical Wedge Volume and Area Calculator and Equation Volume Equation and Calculator of Spherical Wedge |
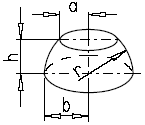 |
Spherical Zone Volume and Area Calculator and Equation Volume Equation and Calculator of Spherical Zone |
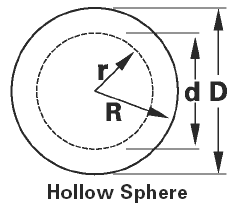 |
Hollow Sphere Volume Equation and Calculator Volume Equation and Calculator of Hollow Sphere |
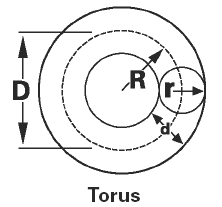 |
Torus Volume and Area Equation and Calculator Volume Equation and Calculator of Circular Torus or Donut |
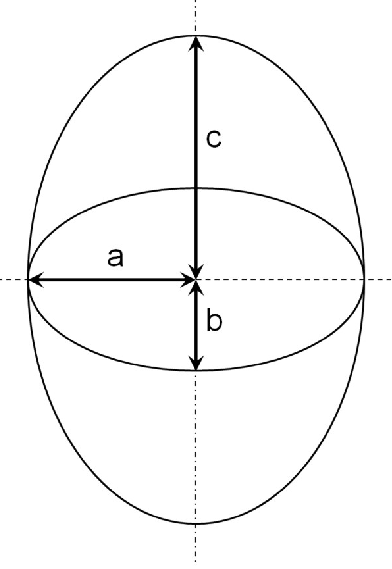 |
Volume of a Ellipsoid Calculator |