Reynolds Number Equation and Review
The flow regime (either laminar or turbulent) is determined by
evaluating the Reynolds number of the flow
refer to (Flow Velocity profiles). The Reynolds
number, based on studies of Osborn
Reynolds, is a dimensionless number
comprised of the physical characteristics of the flow. Equation 3-7 is used
to calculate the Reynolds number (NR)
for fluid flow.
he Reynolds number is defined as the ratio of inertial forces to viscous forces and consequently quantifies the relative importance of these two types of forces for given flow conditions. Reynolds numbers frequently arise when performing scaling of fluid dynamics problems, and as such can be used to determine dynamic similitude between two different cases of fluid flow. They are also used to characterize different flow regimes within a similar fluid, such as laminar or turbulent flow :
- laminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and is characterized by smooth, constant fluid motion;
- turbulent flow occurs at high Reynolds numbers and is dominated by inertial forces, which tend to produce chaotic eddies , vortices and other flow instabilities.
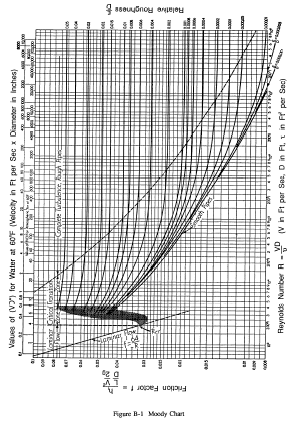
For practical purposes, if the Reynolds number is less than
2000, the flow is laminar. If it is greater
than 3500, the flow is turbulent. Flows with Reynolds numbers between 2000 and
3500 are sometimes referred to as
transitional flows. Most fluid systems in nuclear facilities operate with
turbulent flow. Reynolds numbers can be conveniently determined using a Moody
Chart; an example of which is shown in
figure B-1. Additional detail on the use of the Moody Chart is
provided in subsequent text.
Reynolds Number for a Pipe or Duct in Imperial Units
The Reynolds number for a pipe or duct can also be expressed in Imperial units
Re = (7745.8) u d / ν
where
Re = Reynolds Number (non dimensional)
u = Velocity (ft/s)
d = Pipe diameter (in)
ν = Kinematic Viscosity (cSt) (1 cSt = 10 -6 m2/s )
|
