Standard Deviation Equation and Calculator
Tolerances, Engineering Design & Limits & Fits
This calculator will determine the Standard Deviation from a know set of measurements.
The mathematical formula used calculates one standard deviation, which represents approximately 32 per cent of the points that will fall within the normal curve, as shown in Fig. a. One standard deviation is also called one sigma, or 1σ. Plus or minus one sigma (±1σ) represents 64 per cent of all the points under the normal curve. A wider range on the curve, ±2σ, means that 95.44 per cent of the points are within the normal curve, and ±3σ means that 99.74 per cent of the points are within the normal curve. If an infinite number of runs were made, almost all the measurements would fall within the ±3σ range.
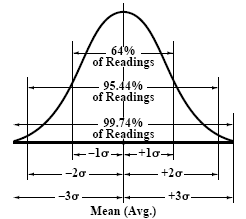
Figure a
Percentages of Points Falling in the ±1σ (64%), ±2σ (95.44%), and ±3σ (99.74%) Ranges
Embed this Standard Deviation Calculator in your Website Code
Related:
Link to this Webpage:
© Copyright 2000 -
2023, by Engineers Edge, LLC
www.engineersedge.com
All rights reserved
Disclaimer |
Feedback
Advertising
| Contact
