Related Resources: calculators
Solid Thin Uniform Disk Rotating External Pressure Stress
Engineering Analysis
Strength and Mechanics of Materials Menu
Solid Thin Uniform Disk Rotating at ω rad/s Under External Pressure po Stress Equations and Calculator
Preview: Solid Thin Uniform Disk with External Pressure Rotating Stress Calculator
The stresses are
The radial stress at any radius r Forumula
Eq. 1
σr = -po + ρ ω2 ( ( 3 + v ) / 8 ) ( ro2 - ri2 )
The tangential stress at any radius r
Eq. 2
σθ = -po + ρ ω2 ( ( 3 + v ) / 8 ) ( ro2 - ( 1 + 3 v ) / ( ( 3 + v ) )
The maximum radial stress at r = 0
Eq. 3
σr(max) = - ρ + ρ ω2 ( 3 + v ) / 8 ro2
The maximum radial stress at r = ro
Eq. 4
σr = -po
The maximum tangential stress at r = 0
Eq. 5
σθ(max) = σr(max)
The displacement u at any radius r
Eq. 6
u = ( r / E ) ( 1 - v ) { -po + ρ ω2 / 8 [ ( 3 + v ) ro - ( 1 - v )r2 ] }
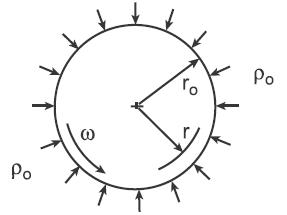
Figure 1 Rotating disk of uniform thickness under external pressure.
where
E = modulus of elasticity or Young’s modulus, Pa [psi (lb/in2)]
r = radius to the stress element under consideration, m (in)
ro = outside radius, m (in)
ρ = mass density, kg/m3 (lbm/in3)
po = pressure, Pa [psi (lb/in2)]
ω = angular velocity of the ring, rad/s
v = Poisson's ratio
u = displacement, m (in)
Related:
- Hollow Cylinder Rotating Stress Equations and Calculator
- Rotating Solid Cylinder Stress Equations and Calculator
- Rotating Rings Bodies Stress Equations and Calculator
- Cylinder Stress and Deflection Rotation Equation and Calculator
- Critical Speeds of Rotating Shafts and Mass Review
- Critical Speeds of Rotating Shafts with Single Loads Equations and Calculators
- Stresses in Rotating Disks (Annular Rings) of Constant Thickness Equation and Calculator
- Beam Deflection and Stress Calculators Formulas & Structural Analysis
Source:
Machine Design Handbook 2nd Edition, 2001
Prof. Dr. K. Lingaiah
Former Principal, Professor and Head, Department of Mechanical Engineering
University Visvesvaraya College of Engineering, Bangalore University, Bangalore