Related Resources: calculators

Stresses in Rotating Disks (Annular Rings) of Constant Thickness Equation and Calculator

Manufacturing, Design and Engineering

Stresses in Rotating Disks (Annular Rings) of Constant Thickness Equation and Calculator

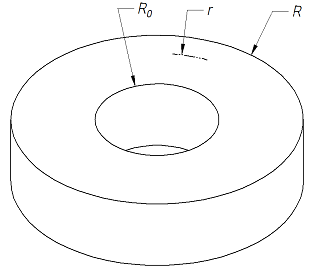
A homogeneous annular disk of uniform thickness outer radius R, and weight per unit volume d, with a central hole of radius R_o, rotates about its own axis with a uniform angular velocity of ω rad/s. At any point a distance r from the center there is a radial tensile inertia stress.

Preview: Stresses in Rotating Disks (Annular Rings) of Constant Thickness Calculator

Radial Tensile Inertia Stress:

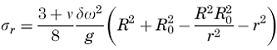
Tangential Tensile Inertia Stress:

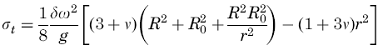
Maximum Radial Stress occurs at r = ( R · R_o )^0.5

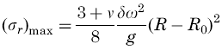
Maximum radial tangential stress occurs at the perimeter of the hole:

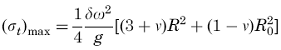
Change in outer radius:

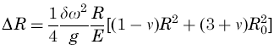
Change in inner radius:

Where:

R = outer radius of disk,(in, m);
R_o = inner radius of disk or radius of bore (in, m);
r = tensile inertia stress at some radial distance (in, m);
δ = Weight per unit volume (lbs/in³, (kg/m³);
g = G Force (386.4 in/s², 9.81456 m/s²)
ω = Angular rotation speed (rad/s);
r_pm = revolutions per minute
E = Elastic Modulus (psi, Pa);
v = Poisson's ratio.

Conversion:

1 rad/sec = 9.549296596425384 rpm
1 rpm = 0.104719755 rad/sec

Reference: Roark's Formulas for Stress and Strain, 7th Edition
Page 746