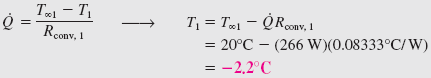Related Resources: heat transfer
Single-Pane Window Heat Loss Equation and Calculator
Heat Transfer Engineering
Thermodynamics
Engineering Physics
Heat Loss through a Single-Pane Window Equation and Calculator
ALL calculators require a Premium Membership
Preview: Heat Loss Through a Single-Pane Window Calculator
![]()
![]()
![]()
![]()
![]()
Where:
Q = Heat Steady State Transfer (W)
A = Area (m2)
k = Thermal Conductivity (W/m · °C)
T∞1 = Temperature (°C)
T∞2 = Temperature (°C)
h1 = Heat Transfer Coefficient (W/m2 · °C)
h2 = Heat Transfer Coefficient (W/m2 · °C)
Rconv, 1 = Thermal Resistance (°C/W)
Rconv, 2 = Thermal Resistance (°C/W)
Rglass = Thermal Resistance Glass (°C/W)
Example:
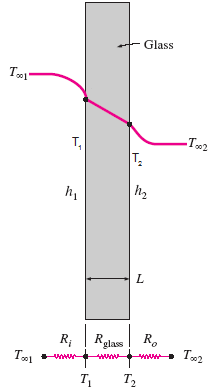
0.8-m-high and 1.5-m-wide glass window with a thickness of 8 mm and a thermal conductivity of k = 0.78 W/m · °C. Determine the steady rate of heat transfer through this glass window and the temperature of its inner surface for a day during which the room is maintained at 20°C while the temperature of the outdoors is -10°C. Take the heat transfer coefficients on the inner and outer surfaces of the window to be h1 = 10 W/m2 · °C and h2 = 40 W/m2 · °C, which includes the effects of radiation.
Assumptions
1 Heat transfer through the window is steady since the surface temperatures remain constant at the specified values.
2 Heat transfer through the wall is one-dimensional since any significant temperature gradients will exist in the direction from the indoors to the outdoors.
3 Thermal conductivity is constant.

all three resistances are in series, the total resistance is
![]()
steady rate of heat transfer through the window becomes
![]()
Knowing the rate of heat transfer, the inner surface temperature of the window glass can be determined from