Horizontal Concentric Cylinders Natural Convection Equations and Calculator

Related Resources: heat transfer

Horizontal Concentric Cylinders Natural Convection Equations and Calculator

Heat Transfer Engineering
Thermodynamics
Engineering Physics

Natural Convection of a Horizontal Concentric Cylinders Equation and Calculator

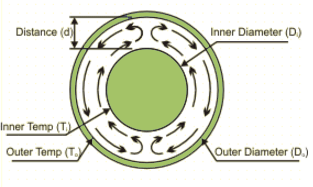
Natural convection heat transfer between two concentric cylinders maintained at constant temperatures. The calculation is based on Rayleigh number and is valid for Rayleigh numbers below 10⁷

Natural Convection of a Horizontal Cylinder Equation and Calculator

ALL calculators require a Premium Membership

Preview: Natural Convection of a Horizontal Concentric Cylinders Calculator

Heat transfer between cylinders calculated from:
q_c = 2 · Π · L · k_eff · (T_i - T_o ) / ln(D_o /D_i )

Where:

k_eff / k = 0.386 · (Ra_c)^(1/4) · (Pr / (0.861 + Pr))^(1/4)

valid between 10² < Ra_c < 10⁷

k_eff = < r below 10² , k_eff = k

Ra_c = Ra_d · (ln(D_o /D_i ))⁴ / (d³ (D_i^-3/5 + D_o^-3/5 )⁵ )

Ra_d= g · cte · ρ² · C_p · (T_i - T_o) · d³/ k · v

Film Temperature
T_f = ( T_p - T_a ) / 2

Fluid density at the film temperature is automatically calculated from the following relationship based on the perfect gas law:

ρ = ρ_ref (T_ref + 273) / (T_f + 273)

Prandtl Number
Pr = v / α

α = k / (ρ · Cp)

v = μ / ρ

Surface Area of Cylinder

A = Π · 2 · (D/2) · L + 2 · Π · (D/2)²

Convective Heat Transfer
q_conv = h ·A · ( T_c - T_a )

Radiative heat transfer
q_rad = σ · A · e · ( T_c⁴ - T_a⁴ )

Total Heat Transfer
q_tot = q_conv + q_rad

Where:

T_f = Film temperature °C
T_c = Cylinder temperature °C
T_a = Ambient Temperature °C
T_ref = Reference Temperature °C
C_p = Specific Heat J/kg- °C
cte = Coefficient of thermal expansion (1/K)
k = Thermal Conductivity (W/m - °C)
μ = Dynamic Viscosity ( kg/m-s )
ρ = Density (kg/m³)
ρ_ref = Density (kg/m³)
Nu = Nusselt Number
D = Diameter of Cylinder (m)
L = Length of Cylinder (m)
A = Surface Area of Cylinder (m² )
e = Emissivity
Pr = Prandtl number
Ra_D = Raleigh number - for a fluid is a dimensionless number associated with buoyancy-driven flow, also known as free convection or natural convection.
h = Average heat transfer coefficient (W/m² - °C)
g = 9.81 (m/s²)
h = Average Heat Transfer (W/m² - °C )
σ = .00000005678 0r 5.678 x 10^-8
q_c = Total uniform heat load on Cylinders (W)

References

Raithby, G. D., and K. G. T. Hollands, A General Method of Obtaining Approximate Solutions to Laminar and Turbulent Free Convection Problems, in T. F. Irvine and J. P. Hartnett, Eds., Advances in Heat Transfer, Vol. 11, Academic Press, New York, pp 265-315, 1975.

Incropera, De Witt., Fundamentals of Heat and Mass Transfer , 3rd ed., John Wiley & Sons, p563, eq 9.58-9.60, 1990.