Related Resources: calculators
Elastic Frame Concentrated Load Reaction and Deflection Equations and Calculator
Beam Deflection and Stress Equation and Calculators
Concentrated Load on the Horizontal Member Elastic Frame Equations and Calculator
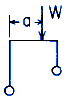
Loading Configuration
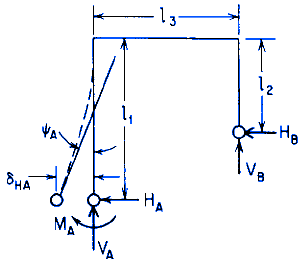
General Designations
ALL calculators require a Premium Membership
Preview
Concentrated load on the Horizontal member elastic frames calculator:
General reaction and deformation expressions with right and left ends pinned
Horizontal Deflection at A:
![]()
Reaction locations are pinned therefore, the displacements = 0 = δHA
Angular Rotation at A:
![]()
Where:
![]()
![]()
![]()
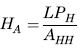
![]()

Va = W (l3 - a)/ l3
Vb = W a / l3
Reaction locations are pinned therefore, the Moments = 0 = MA = MB
Where:
W = Load or Force (lbsf, N),
w = Unit Load or force per unit length (lbs/in2, N/mm2)
Mo = Applied couple (moment) ( lbs-in, N-mm),
θo = Externally created angular displacement (radians),
Δo, = Externally created concentrated lateral displacement (in, mm),
T - To = Uniform temperature rise (Deg.),
T1, T2 = Temperature on outside and inside respectively (degrees),
HA, HB = Horizontal end reaction moments at the left and right, respectively, and are positive clockwise (lbs, N),
I1, I2, and I3 = Respective area moments of inertia for bending in the plane of the frame for the three members (in4, mm4),
E1, E2, and E3 = Respective moduli of elasticity (lb/in2, Pa) Related: Modulus of Elasticity, Yield Strength;
γ1, γ2, and γ3 = Respective temperature coefficients of expansions unit strain per. degree ( in/in/°F, mm/mm/°C),
l1, l2, l3 = Member lengths respectively (in, mm),
References:
Roark's Formulas for Stress and Strain