Diameter Change Press and Shrink Fit Formulae and Calculator

Related Resources: calculators

Diameter Change Press and Shrink Fit Formulae and Calculator

Beam Deflection and Stress Calculators with Formulas
Strength and Mechanics of Materials Menu

Diameter Change for Cylinder Press and Shrink Fits Analysis Equations and Calculator

Premium membership required for access to calculator

Preview Diameter Change for Cylinder Press and Shrink Fits Analysis Calculator

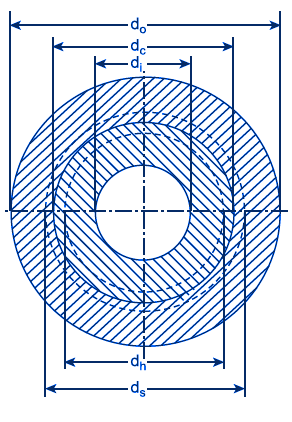
Figure 1 Press Fit Cylinders Contact and Interference

Change in Diameter
Eq. 1
Δd = d ε_θ

The change in diameter of the inner member when subjected to contact pressure p_c
Eq. 2
Δd_i = - ( p_c d_c ) / E [ ( d_c² + d_i² ) / ( d_c² - d_i² ) -v ]

The change in diameter of the outer member when subjected to contact pressure p_c
Eq. 3
Δd_o = ( p_c d_c ) / E [ ( d_o² + d_c² ) / ( d_o² - d_c² ) +v ]

The original difference in diameters of the two cylinders when the material of the members is the same
Eq. 4
δ = Δd_o + Δd_i

Eq. 4a
Δd_o = p_c d_c / E [ ( d_o² + d_c² ) / ( d_o² - d_c² ) +v ]

Eq. 4b
Δd_i = p_c d_c / E [ ( d_c² + d_i² ) / ( d_c² - d_i² ) -v ]

The total change in the diameters of hub and hollow shaft due to contact pressure at their contact surface when the material of the members is the same
Eq. 5
δ = Δd_s + Δd_h = d_s - d_h

Eq. 5a
Δd_s = p_c d_s / E_s [ ( d_s² + d_i² ) / ( d_s² - d_i² ) - v_s ]

Eq. 5b
Δd_h = p_c d_h / E_h [ ( d_o² + d_h² ) / ( d_o² - d_s² ) - v_h ] exactly

Eq. 5c
δ = p_c d_c / [ ( d_c² + d_i² ) / ( E_s ( d_c² - d_i² ) ) -v ] + p_c² d_c / E_h [ ( d_o² + d_h² ) / ( d_o² - d_s² ) - v ]

Eq. 5d - (approx.)
p_c d_c = [ ( d_c² + d_i² ) / ( E_s ( d_c² - d_i² ) ) + ( d_o² + d_c² ) / ( E_h ( d_o² - d_c² ) ) - v_s / E_s + v_h / E_h )

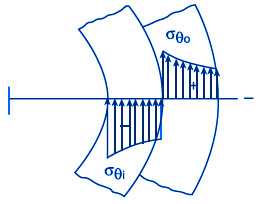
Figure 2 Tangential stress, σ_θ

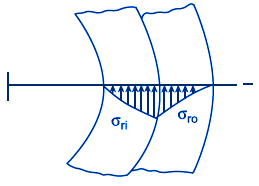
Figure 3, radial stress σ_r

The shrinkage stress in the band (Fig. 2 & 3)
Eq. 6
σ_θ = E δ / d_c

The contact pressure between cylinders at the surface of contact when the material of both the cylinders is same (Fig. 2)
Eq. 7
p_c = ( E δ ( d_c² - d_i² ) ( d_o² - d_c² ) ) / ( 2 d_c³ ( d_o² - d_i² ) )

The tangential stress at any radius r of outer cylinder (Fig. 2)
Eq. 8
σ_θ-o = p_c d_c² / ( d_o² - d_c² ) [ 1 + d_o² / ( 4 r_o² ) ]

The tangential stress at any radius r of inner cylinder (Fig. 2)
Eq. 9
σ_θ-i = - p_c d_c² / ( d_o² - d_c² ) [ 1 + d_i² / ( 4 r_i² ) ]

The radial stress at any radius r of outer cylinder (Fig. 2)
Eq. 10
σ_θ-o = - p_c d_c² / ( d_o² - d_c² ) [ d_o² / ( 4 r_o² ) -1 ]

The radial stress at any radius r of inner cylinder (Fig. 2)
Eq. 11
σ_θ-i = p_c d_c² / ( d_c² - d_i² ) / 1 - d_i² / ( 4 r_i² ) ]

The tangential stress at outside diameter of outer cylinder (Fig. 2 & 3)
Eq. 12
σ_θ-oo = 2 p_c d_c² / ( d_o² - d_c² )

The tangential stress at inside diameter of outer cylinder (Fig. 2 & 3)
Eq. 13
σ_θ-oi = p_c [ ( d_o² + d_c² ) / ( d_o² - d_c² ) ]

The tangential stress at outside diameter of inner cylinder (Fig. 2 & 3)
Eq. 14
σ_θ-io = - p_c [ ( d_c² + d_i² ) / ( d_c² - d_i² ) ]

The tangential stress at inside diameter of inner cylinder (Fig. 2 & 3)
Eq. 15
σ_θ-ii = - 2 p_c d_c² / ( d_c² - d_i² )

The radial stress at outside diameter of outer cylinder (Fig. 2 & 3)
Eq. 16
σ_r-oo = 0

The radial stress at inside diameter of outer cylinder (Fig. 2 & 3)
Eq. 17
σ_r-oi = - p_c

The radial stress at outside diameter of inner cylinder (Fig. 2 & 3)
Eq. 18
σ_r-io = - p_c

The radial stress at inside diameter of inner cylinder (Fig. 2 & 3)
Eq. 19
σ_r-ii = 0

The semiempirical formula for tangential stress for cast-iron hub on steel shaft
Eq. 20
σ_θ = E_o δ / ( d_c + 0.14 d_o )

Timoshenko equation for contact pressure in case of steel shaft on cast-iron hub
Eq. 21
p_c = E_o δ / d_c [ ( 1 - ( d_c / d_o )² ) / ( 1.53 + 0.47 ( d_c / d_o )² ) ]
for E_s / E_c = 3

The allowable stress for brittle materials
Eq. 22
σ_all = σ_su / n = [ ( E_c δ ( 1 + ( d_c / d_o )² ] / ( d_c [ 1.53 + 0.47 ( d_c / d_o )² ]

where

d_s = shaft outer diameter, m (in)
d_i = shaft inner diameter, m (in)
d_o = Outer hub diameter, m (in)
d_h = Outer hub inner diameter, m (in)
r_o = radius within outer cylinder material, m (in)
r_i = radius within inner cylinder material, m (in)
d_c = contact surface diameter, compressive, m (in)
p_c = contact pressure MPa (psi)
σ = stress, MPa (psi)
δ = total change in diameter (interference), m (in)
E = modulus of elasticity, GPa (Mpsi)
E_h = modulus of elasticity of cast iron, GPa (Mpsi)
E_s = modulus of elasticity of steel, GPa (Mpsi)
v = Poisson’s ratio
n = factor of safety

Source:

Machine Design Handbook 2nd Edition, 2001
Prof. Dr. K. Lingaiah
Former Principal, Professor and Head, Department of Mechanical Engineering
University Visvesvaraya College of Engineering, Bangalore University, Bangalore