Related Resources: calculators
Concentrated Angular Displacement Left Vertical Member 9 Deflections Equation and Calculator
Beam Deflection and Stress Equation and Calculators
Reaction and deflection formulas for in-plane loading of elastic frame.
Concentrated Angular Displacement on Left Vertical Member Elastic Frame Deflection Left Vertical Member Guided Horizontally, Right End Pinned Equation and Calculator.

Loading Configuration
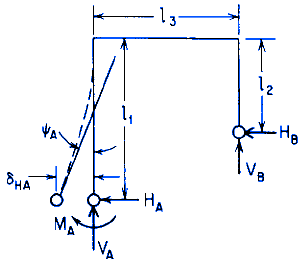
General Designations
ALL calculators require a Premium Membership
Preview
Frame Deflections with Concentrated Angular Displacement Calculator:
Since ψA = 0 and HA = 0
MA = LPM / AMM = Moment (Couple) at Left Node A
δHA = AHM MA - LPH = Horizontal Deflection at Left Node A
Where:
![]()
![]()
![]()
Loading Terms LPH and LPM are given below.
Reaction loads and moments VA and VB, and HB can be evaluated from equilibrium equations after calculating HA and MA.
Note: Δo could also be an increase in the length l1 or a decrease in the length l2.
LPH = θo (a)
LPM = 0
Where:
Δo = Displacement (in, mm),
θo = Angular Displacement (radians),
W = Load or Force (lbsf, N),
w = Unit Load or force per unit length (lbs/in2, N/mm2),
MA = Couple (moment) ( lbs-in, N-mm),
Mo = Couple (moment) ( lbs-in, N-mm),
θo = Externally created angular displacement (radians),
Δo, = Externally created concentrated lateral displacement (in, mm),
T1 - T2 = Uniform temperature rise (°F),
To = Average Temperature (deg °F),
γ = Temperature coefficient of expansion [ µinch/(in. °F), µmm/(mm. °F) ],
T1, T2 = Temperature on outside and inside respectively (degrees),
HA, HB = Horizontal end reaction moments at the left and right, respectively, and are positive clockwise (lbs, N),
I1, I2, and I3 = Respective area moments of inertia for bending in the plane of the frame for the three members (in4, mm4),
E1, E2, and E3 = Respective moduli of elasticity (lb/in2, Pa) Related: Modulus of Elasticity, Yield Strength;
γ1, γ2, and γ3 = Respective temperature coefficients of expansions unit strain per. degree ( in/in/°F, mm/mm/°C),
l1, l2, l3 = Member lengths respectively (in, mm),
References:
Roark's Formulas for Stress and Strain, Seventh Edition