Related Resources: beam bending

Double Integration Method Example 3 Proof Cantilevered Beam

Beams Deflection and Stress Formulas and Calculators
Engineering Mathematics

Double Integration Method Example 3 Proof Cantilevered Beam of Length L with Variable Increasing Load to ω_o at free end.

The Double Integration Method, also known as Macaulay’s Method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.

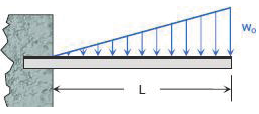
Elastic Curve

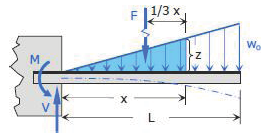
Equations of elastic curve

V = ½ ω_o L

M = ½ ω_o L [ (2/3) L]

M = (1/3) ω_o L²

By ratio and proportion

z / x = ω_o / L

z = x ( ω_o / L )

F = ½ x z

F = ½ x ( x ( ω_o / L ) )

F = ( ω_o / ( 2 L ) ) x²

E I y'' = -M + V x - F ( x / 3 )

E I y'' = -( 1 / 3 ) ω_o L² + 0.5 ω_o L x - (1/3) x ( ω_o / ( 2 L ) x² )

E I y'' = - ω_o L² / 3 + ( ( ω_o L ) / 2 ) x- ω_o / ( 6 L ) x³

E I y' = - ( ω_o L² / 3 ) x + ( ω_o L / 4 ) x² - ω_o / ( 24 L ) x⁴ + C₁

E I y = - ( ω_o L² / 6 ) x² + ( ω_o L / 12 ) x³ - ω_o / ( 120 L ) x⁵ +C₁ x + C₂

At x = 0, y' = 0, therefore C₁ = 0
At x = 0, y = 0, therefore C₂ = 0

Therefore, the equation of the elastic curve is

E I y = - ( ω_o L² / 6 ) x² + ( ω_o L / 12 ) x³ - ω_o / ( 120 L ) x⁵

Related:

• Double Integration Method for Beam Deflections
• Double Integration Method Example 1 Simply Supported Beam of Length L with Concentrated Load at Mid Span
• Beam Supported on Both Ends Uniform Loading Deflection and Stress Stress, Deflection Equation and Calculator using total applied load and line load.
• Beam Calculator Cantilevered Beam with One Load Applied at End Deflection and Stress Structural Beam Deflection, Stress, Bending Equations and calculator for a Cantilevered Beam with One Load Applied at End.
• Beam Distributed Load Deflection, Shear, Deflection and Stress Equations and Calculator Beam Deflection, Shear and Stress Equations and Calculator for a Beam supported One End, Pin Opposite End and Partial Distributed Load
• Calculator for a Beam supported One End, Pin Opposite End and Single Moment at End Applied Deflection and Stress Calc Beam Deflection, Shear and Stress Equations and Calculator for a Beam supported One End, Pin Opposite End and Single Moment at End Applied
• Stress & Deflection Deflection Equations and Calculator Beam Supported Uniform loading Applied on Cantilevered End Stress Deflection Equations and Calculator Beam Supported Uniform loading Applied on Cantilevered End

Reference:

• Dr. ZM Nizam Lecture Notes
• Shingley Machine Design, 4-3 "Deflection Due to Bending"
• Beam Deflection by Integration Lecture Presentation Paul Palazolo, University of Memphis,
• Beam Deflections Using Double integration, Steven Vukazich, San Jose University