Related Resources: beam bending
Double Integration Method for Beam Deflections
Beams Deflection and Stress Formulas and Calculators
Engineering Mathematics
Double Integration Method for Beam Deflections Overview
The Double Integration Method, also known as Macaulay’s Method is a powerful tool in solving deflection and slope of a beam at any point because we will be able to get the equation of the elastic curve.
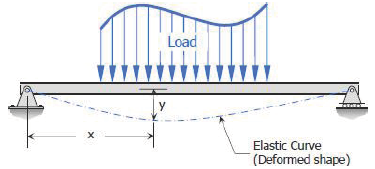
Elastic Curve
There are numerous methods are available for the determination of beam deflections. These methods include:
- Double Integration Method
- Moment Area Method
- Strain Energy Method (Castigliano’s Theorem)
- Conjugate Beam Method
Of these methods, the first two are the ones that are commonly used.
Double Integration Method
In calculus, the radius of curvature of a curve y = f(x) is given by
![]()
The radius of curvature of a beam is given as:
![]()
Deflection of beams is so small, such that the slope of the elastic curve dy/dx is very small, and squaring this expression the value becomes practically negligible, hence
![]()
Thus, EI / M = 1 / y''
![]()
If EI is constant, the equation may be written as:
![]()
where x and y are the coordinates shown in the beam image given above of the elastic curve of the beam under load, y is the deflection of the beam at any distance x. E is the modulus of elasticity of the beam, I represent the moment of inertia about the neutral axis, and M represents the bending moment at a distance x from the end of the beam. The product EI is called the flexural rigidity of the beam.
The first integration y' yields the slope of the elastic curve and the second integration y” gives the deflection of the beam at any distance x. The resulting solution must contain two constants of integration since EI y" = M is of second order. These two constants must be evaluated from known conditions concerning the slope deflection at certain points of the beam. For instance, in the case of a simply supported beam with rigid supports, at x = 0 and x = L, the deflection y = 0, and in locating the point of maximum deflection, we simply set the slope of the elastic curve y' to zero.
Reference:
- Dr. ZM Nizam Lecture Notes
- Shingley Machine Design, 4-3 "Deflection Due to Bending"
- Beam Deflection by Integration Lecture Presentation Paul Palazolo, University of Memphis,
- Beam Deflections Using Double integration, Steven Vukazich, San Jose University
Related
- Beam Stress and Deflection Equation and Calculator Structural Beam Deflection, Stress, Bending Equation and Calculator for a Beam with Ends Overhanging Supports and Two loads.
- Cantilevered Beam Stress & Deflection Equations and Calculator Deflection and Stress Structural Beam Deflection, Stress, Bending Equations and calculator for a Cantilevered Beam with Load at Location Between Support and Load.
- Curved I-Beam Stress Formulas and Calculator
- Double Integration Method Example 5 Proof Pinned Supported Beam
- Double Integration Method Example 4 Proof Simply Supported Beam of Length L with Partial Distributed Load
- Double Integration Method Example 1 Simply Supported Beam with Concentrated Load at Mid Span
- Calculus Applications and Basics