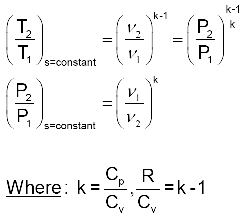Isentropic Process Thermodynamics - Thermodynamics
Thermodynamics Directory
Heat Transfer Directory
An isentropic process is one in which the entropy of the fluid remains constant. This will be true if the process the system goes through is reversible and adiabatic. An isentropic process can also be called a constant entropy process.
Isentropic Processes of Ideal Gases with Constant Specific Heats Equations:
Where: R = Cp - Cv
Isentropic Processes of Ideal Gases with Constant Specific Heats –More Common Form.
These can be simplified to: