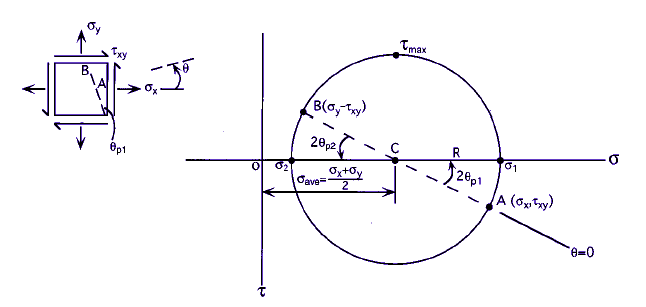
|
The equations for plane stress transformation have a graphical solution, called Mohr’s circle, which is
convenient to use in engineering practice, including “back-of-the-envelope” calculations.
Mohr’s circle
is plotted on a coordinate system:
as in the illustration below, with the center C of the circle always on the:
 axis at 
The positive  axis is downward
for convenience, to make  on the element and the corresponding 2 on the circle agree in sense (both
counterclockwise here).
1. The center C of the circle is always on the axis, but it may move left and right in a dynamic
loading situation. This should be considered in failure prevention.
2. The radius R of the circle is  , and it may change, even pulsate, in dynamic loading. This is
also relevant in failure prevention.
3. Working back and forth between the rectangular element and the circle should be done carefully
and consistently. An angle on the element should be represented by 2 in the corresponding
circle. If is positive downward for the circle, the sense of rotation is identical in the element
and the circle.
4. The principal stresses 1 and 2 are on the axis ( = 0).
5. The planes on which 1 and 2 act are oriented at  from the planes of x and y (respectively)
in the circle and at  in the element.
6. The stresses on an arbitrary plane can be determined by their and coordinates from the circle.
These coordinates give magnitudes and signs of the stresses. The physical meaning of + vs. –
regarding material response is normally not as distinct as + vs. – (tension vs. compression).
7. To plot the circle, either use the calculated center C coordinate and the radius R, or directly plot
the stress coordinates for two mutually perpendicular planes and draw the circle through the two
points (A and B in illustration above) which must be diametrically opposite on the circle.
Related:
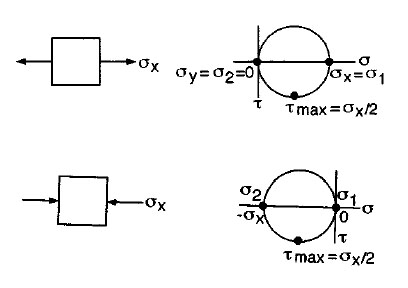
Special Cases of Mohr’s Circles for Plane Stress
 |
Uniaxial Tension |
| Uniaxial Tension |
|
 |
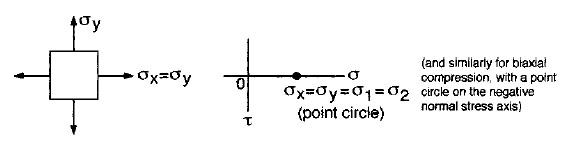Pure Shear |
 |
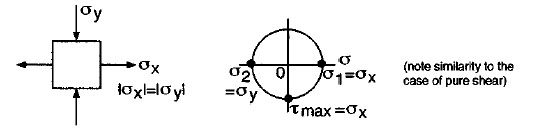Biaxial tension-compression:
(similar to the case of pure shear). |
|
