Related Resources: fluid flow
Surface Tension of Water, Salt and Fresh
Surface Tension of Water, Salt and Fresh :
Vargaftik et al. (1983) tabulate consensus values for the surface tension of pure water for temperatures between 0°C and the critical temperature, 374°C (Bohren and Albrecht 1998, p. 207ff.). They also develop from these data the following relation for computing the surface tension of pure water:
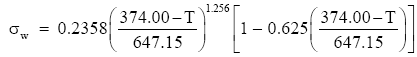
(Eq 1)
This gives σw in J m-2 when the water temperature T is in °C. This equation predicts exactly the values of surface tension that Lide (2001, p. 6-3) tabulates and matches the values in Batchelor (1970, p. 597) to within about 0.1%.
For temperatures between −45° and 0°C, Pruppacher and Klett (1997, p. 130) suggest computing the surface tension of pure water from
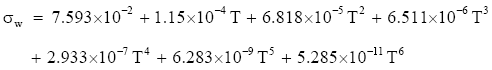
(Eq 2)
which again gives σw in J m−2 for T in °C. Unfortunately, (Eq 1) and (Eq 2) do not meet at 0°C. Equation (Eq 1) predicts 7.656 × 10-2 J m-2 there, while (Eq 2) gives 7.593 × 10-2 J m-2. The former value is probably the more accurate one.
Pruppacher and Klett (1978, p. 107) likewise give an expression for the surface tension of an interface between water vapor and saline water. That expression, however, quantifies the salinity in terms of ms/mw, where mw is the mass of pure water per unit volume and ms is the mass of dissolved salt in the volume. Since the definition of salinity is
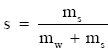
(Eq 3)
we see that
![]()
(Eq 4)
where s is the fractional salinity [s = S(in psu)/1000].
Hence, I convert Pruppacher and Klett’s (1978) expression for the surface tension at a seawater interface to
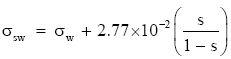
(Eq 5)
where σw comes from (Eq 1) or (Eq 2), depending on the water temperature. The coefficient multiplying the salinity term in (Eq 5) is virtually the same value that Hänel (1976) recommends. Equation (Eq 5) should be accurate for temperatures in [−25°, 40°C] and S in [0, 260 psu].