Related Resources: fluid flow

Convergent Nozzle Flow Velocity and Area Equation and Calculator

Hydraulic & Pneumatics
Fluids Design and Engineering Data

Convergent Nozzle Flow Velocity and Area Equation and Calculator

Nozzles are used in steam and gas turbines, in rocket motors, in jet engines and in many other applications. Two types of nozzle are considered: the ‘convergent nozzle’, where the flow is subsonic; and the ‘convergent divergent nozzle’, for supersonic flow.

Outlet pressure p₂ greater than p_c, i.e. r > r_c

 

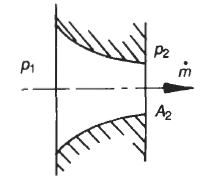
Nozzle Outlet Velocity Equation

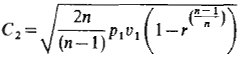
Nozzle Critical Pressure Ratio:

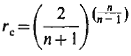
Nozzle Outlet Area Equation

When Outlet pressure p₂ equal to or less than p_c, i.e. r ≤ r_c the following equation applies;

Nozzle Outlet Velocity Equation

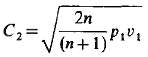
Note that C₂ is independent of p₂ and that the nozzle flow is a maximum. In this case the nozzle is said to be ‘choked’.

where:

p₁ = Inlet pressure (N / m², Pa)
p₂ = Outlet pressure (N / m², Pa)
p_c = critical pressure at throat (N / m², Pa)
v₁ = Inlet specific volume (m³)
v_c = Outlet specific volume (m³)
C₂ = Outlet velocity (m/sec)
C_c = Throat velocity (m/sec)

r = pressure ratio = p₁ / p₂

r_c = critical pressure ratio

A₂ = outlet area (m²)
A_c = throat area (m²)
n = index of expansion
m = mass flow rate (kg/m²)

Fluid	n	rc
Air (n = γ)	1.40	0.528
Initially dry saturated steam	1.135	0.577
Initially superheated steam	1.30	0.546