Related Resources: civil engineering
Flow over Channel Rise Hump Formula
Flow over Channel Rise Hump Formula
In the case of flow in a constant width (b) horizontal rectangular channel with a small rise on the floor (Figure 1),
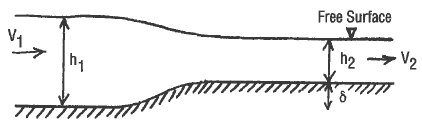
Figure 1, Open-channel flow over a rise.
the relations are:
Eq. 1
V12 / 2 + g h1 = V22 / 2 + g ( h2 δ )
Eq. 2
Q = V1 b h1 = V2 b h2
Q2 / ( 2 g b2 h12 ) = h1 Q2 / ( 2 g b2 h22 ) + ( h2 + δ )
Note that the sum of the two terms h + Q2 / ( 2 g b2 h22 ) is called the specific head, H. The critical specific head H, and the critical depth h, can be found by taking the derivative of above term and equating it to zero.
hc3 = Q2 / ( g b2 )
Hc = 3 hc / 2
Note that for a given specific head and flow rate, two different depths of h are possible. The Froude n d e r V/(gh) specifies the flow characteristics of the channel flow. If it is less than unity, it is called subcritical, or tranquil, flow. If it is more than unity, it is called supercritical, or rapid, flow.
Where:
Q = flow, ( ft3 / sec, m3 / sec)
V1 = flow velocity, (ft / sec, m / sec)
V2 = flow velocity, (ft / sec, m / sec)
g = Gravity (32.2 ft/sec2 , 9.81 m/sec2 )
b = channel width, (ft, m)
h1 = height, (ft, m)
h2 = height, (ft, m)
δ = rise, (ft, m)
Hc = critical specific head, (ft, m)
Related:
- Fluid Flow Open Channel Chezy and Manning's Equation Calculator
- Water Flow Over Rectangular Weir Formula and Calculator
- Manning's Roughness Coefficient Chart Table
- Required Flow Velocity in Sewers Formula and Calculator
- Flow Velocity in Straight Sewers Formula and Calculator
- Storm Drain Pipe Size Requirement Formula and Calculator
Reference:
Rules of Thumb for Mechanical Engineers
J. Edward Pope, Editor