Related Resources: calculators

Strain Gage Rosette Equations and Calculator

Strength of Materials
Structural Deflections and Stress Equations and Calculator

Strain gage rosette equations and calculator applied to a specimen of a linear, isotropic material.

Generally, if the direction of principal stress is uncertain in structure stress measurement, a triaxial rosette gage is used and measured strain values are calculated in the following equation to find the direction of the principal stress.

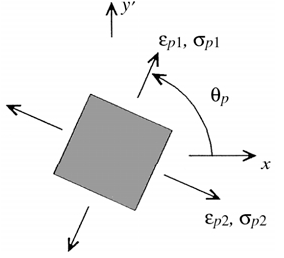
The principal strains and stresses are given relative to the xy coordinate axes as shown below.

 

Preview: Strain Gage Rosette Calculator

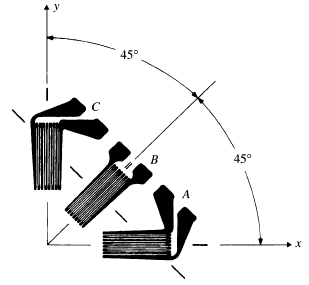
Three-Element Rectangular Rosette

Maximum Principal Strain

Minimum Principal Strain

Principal Stresses:

Maximum Principal Stress

Minimum Principal Stress

Maximum Shearing Stress
τ_max = ( E / ( 2 (1+ν²) ) [ 2 ( ( ε_A - ε_B ) + ( ε_B - ε_C ) ) ]^1/2

Max. Shearing Strain
γ_max = [ 2 { ( ε_A - ε_B )² + ( ε_B - ε_C )² } ]^1/2

Direction of Principal angle from ε_a axis when ε_a > ε_c Angle of minimum principal strain to the ε_a axis when ε_a < ε_c
Treating the tan^-1 as a single-valued function, the angle counterclockwise from gage A to the axis containing ε_p1 or σ_p1 is given by:

Where:

E = Young's Modulus (N/m², lbs/in²)
ν = Poissons Ratio
ε = strain (μm/m, μin/in)
σ = Stress (N/m², lbs/in²)
θ_p = Angle (degrees)

Reference:

Roarks Formulas for Stress and Strain
KYOWA Electronic Instruments