Sprocket Chain Length Formulae and Calculator

Related Resources: calculators

Sprocket Chain Length Formulae and Calculator

Gear Design and Selection Application

Chain Length For Two Sprockets Formulas and Calculator

It is sometimes necessary to fix the center-to-center distance of the sprockets to accommodate existing constraints or mechanical design considerations. An example of this may be the case where a chain and sprocket assembly are fixed to a nonadjustable motor shaft and required to drive a set of meshing gears.

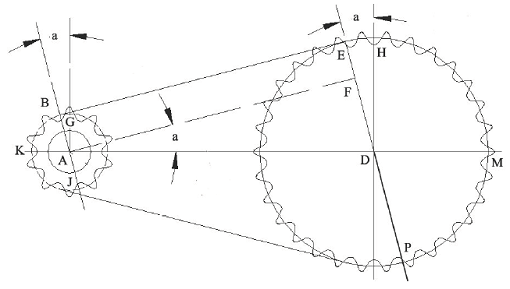
Chain length is a function of the number of teeth of the drive and driven sprockets as well as the center-to-center distance. Here is an example of the process required to calculate chain length given a center distance and the sprocket teeth numbers.

Note: Chain length is customarily expressed in (even numbers) of pitch units since chains can only be shortened or lengthened by multiples of their pitch units. If an odd number of pitches is required then a special link called an offset link is used.

Sprocket Diagram

Preview: Chain Length For Two Sprockets Calculator

Chain Length in Pitch Units For Two Sprockets Equation

L = 2 [ C cos a + ( N + n ) / 4 + ( a / 360 ) ( N- n ) ]

Since each pitch unit represents 1 chain link, and it is not possible to have a fractional link, we must round off the chain length to a whole number. Remember, it is best practice to use EVEN numbers of chain links.

Note: Do not round down. This causes the chain to be too tight and the added tension can damage sprockets, shafts and cause premature chain failure.

Where:

L = Chain length in pitch (Pitch Units),
L_lin = Linear length of chain,
N = Drive Sprocket number of teeth,
n = Driven Sprocket number of teeth,
a = angle (deg) sin a = DF / AD,
P = Pitch of sprockets,
S_d = Linear distance from A to D,
C = Distance From (A to D) / P Center Distance between sprockets expressed in Pitch Units

Reference ANSI/ASME B29.1M