Related Resources: calculators
Prism Refraction Index from Minimum Angle of Deviation Equations and Calculator
Engineering Physics
Engineering and Design Applications
Prism Refraction Index from Minimum Angle of Deviation Equations and Calculator
Also see: Ray Optics Simulation and Calculator
Glass prisms are often used to bend light in a given direction as well as to bend it back again (retroreflection). The process of refraction in prisms is understood easily with the use of light rays and Snell’s law. Look at Figure 1. When a light ray enters a prism at one face and exits at another, the exiting ray is deviated from its original direction. The prism shown is isosceles in cross section with apex angle A = 30° and refractive index n = 1.50. The incident angle θ and the angle of deviation δ are shown on the diagram.
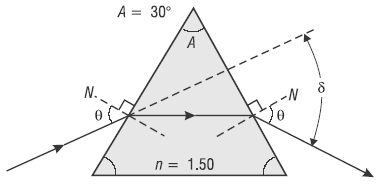
Figure 1 Refraction of light through a prism
Figure 2 shows how the angle of deviation δ changes as the angle θ of the incident ray changes. The specific curve shown is for the prism described in Figure 1. Note that δ goes through a minimum value, about 23° for this specific prism. Each prism material has its own unique minimum angle of deviation.
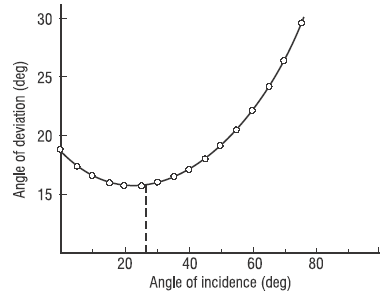
Figure 2 Deviation vs angle of incidence (deg)
Minimum angle of deviation. It turns out that we can determine the refractive index of a transparent material by shaping it in the form of an isosceles prism and then measuring its minimum angle of deviation. With reference to Figure 1, the relationship between the refractive index n, the prism apex angle A, and the minimum angle of deviation δm is given by:
Equation 1
n = [ sin ( A + δm ) / 2 ] / ( sin (A / 2 )
Where:
A and δm are measured in degrees.
The derivation of Equation 1 is straightforward, but a bit tedious. Details of the derivation making use of Snell’s law and geometric relations between angles at each refracting surface can be found in most standard texts on geometrical optics.
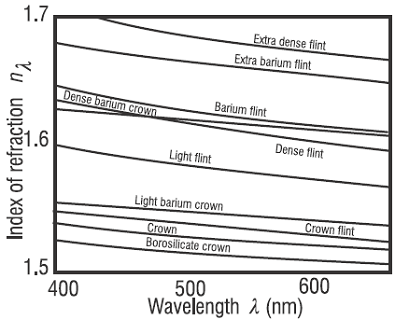
Figure 3 Typical dispersion curves Refraction by a prism

Figure 4 Optical glass dispersion curves
Related:
References:
Fundamentals of Photonics, Leno S. Pedrottie CORD Waco, Texas