Flat Thrust Plate Bearing Design Equation and Calculator

Related Resources: calculators

Flat Thrust Plate Bearing Design Equation and Calculator

Machine Design Applications
Bearing Engineering and Design

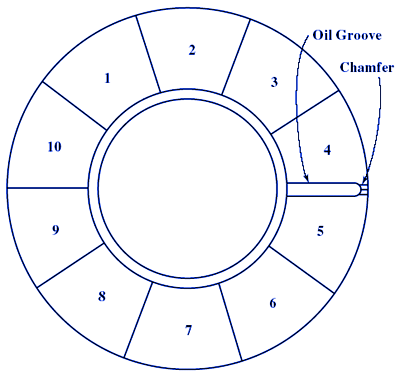
Flat Thrust Plate Bearing Design Equation and Calculator: Fluid thrust bearings contain a number of sector-shaped pads, arranged in a circle around the shaft, and which are free to pivot. These create wedge-shaped regions of oil inside the bearing between the pads and a rotating disk, which support the applied thrust and eliminate metal-on-metal contact. Although each bearing section is wedge shaped, as shown below right, for the purposes of design calculation, it is considered to be a rectangle with a length b equal to the circumferential length along the pitch line of the section being considered, and a width a equal to the difference in the external and internal radii.

Typical Thrust Plate

Basic Element of thrust bearing

Preview: Flat Thrust Plate Bearing Design Calculator

Thrust Bearing Typical Loads
Surface	Loads Lbs/in²	Max Loads Lbs/in²
Parallel surface	< 75	< 150
Step Surface	200	500
Tapered Land Surface	200	500
Tilting Pad Surface	200	500

External diameter formula:

D₂ = ( ( 4 W ) / ( ( π K_g p ) + D₁² )^1/2

Where:

W = applied load, pounds
K_g = fraction of circumference occupied by pads; usually, 0.8
p = bearing unit load, psi

Radial pad width, given in inches

a = (1/2) ( D₂ - D₁ )

Pitch line circumference, given in inches

B = π ( D₂ - a )

Number of bearing pads, i. Assume that the oil groove width, s is minimum

i = B / ( a + s ) = nearest even number

i as the nearest even number to that calculated.

Length of bearing pad given in inches

b = [ B - ( i s ) ] / i

Actual unit load, given in psi

p = W / ( i a b)

Pitch line velocity, given in fpm

U = ( B N ) / 12

where, N - rpm

Friction power loss, given in HP

P_f = i a b M

M = Horsepower Loss per in² derived from:

Friction power loss, M, vs. peripheral speed, U — thrust bearings.chart

Oil flow required, given in gpm

Q = ( 42.4 P_f ) / ( c Δt )

where:

c = Specific heat of oil in Btu/gal/°F
Δt = temperature rise °F

Film flow, given in gpm

Q_f = [ ( 1.5 ) ( 10⁵ ) i V h³ p_s ] / Z₂

Where:

V = effective width-to-length ratio for one pad, a/b
Z₂ = oil viscosity at outlet temperature
h = film thickness
Note: Because h cannot be calculated, use h = 0.002 inch.

Required flow per. chamfer, given in gpm

Q_c = Q / i

Kinetic energy correction factor ξ derived from chart using values Z₂l and Q_c

Kinetic energy correction factor chart

Uncorrected flow per chamfer, given in gpm

Q^o_c = Q_c / ξ

Depth of chamfer, given in inches

g = [ ( Q^o_c l Z₂ ) / ( 4.74 x 10⁴ p_s ) ]^1/4

Flat plate thrust bearing example design.

Notation:

a = radial width of pad, inches
b = circumferential length of pad at pitch line, inches
b₂ = pad step length
B = circumference of pitch circle, inches
c = specific heat of oil, Btu/gal/°F
D = diameter, inches
e = depth of step, inch
f = coefficient of friction
g = depth of 45° chamfer, inches
h = film thickness, inch
i = number of pads
J = power loss coefficient
K = film thickness factor
K_g = fraction of circumference occupied by the pads; usually, 0.8
l = length of chamfer, inches
M = horsepower per square inch
N = revolutions per minute
O = operating number
p = bearing unit load, psi
p_s = oil-supply pressure, psi
P_f = friction horsepower
Q = total flow, gpm
Q_c = required flow per chamfer, gpm
Q^o_c = uncorrected required flow per chamfer, gpm
Q_F = film flow, gpm
s = oil-groove width
∆t = temperature rise, °F
U = velocity, feet per minute
V = effective width-to-length ratio for one pad
W = applied load, pounds
Y_g = oil-flow factor
Y_l = leakage factor
Y_S = shape factor
Z = viscosity, centipoises
α = dimensionless film-thickness factor
δ = taper
ξ = kinetic energy correction factor

References:

Machinery's Handbook, 29th Edition
Understanding Journal Bearings, Malcolm E. Leader, P.E. Applied Machinery Dynamics Co.
Theory and Practice of Lubrication for Engineers by Dudley D. Fuller, Wiley and Sons, 1984, ISBN 0- 471-04703-1
Bearing Design and Application by Donald F. Wilcock and E. Richard Booser, McGraw Hill, 1957, 195, LC number 56-9641