Related Resources: calculators
Circular Ring Stress and Deformations Formulae and Calculator
Circular Ring Moment, Hoop Load, and Radial Shear Equations and Calculator.
Loading W applied at 180° through center of circular section
Per. Roarks Formulas for Stress and Strain Formulas for Circular Rings Section 9
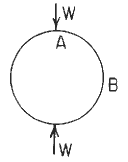 Circular Ring Loading |
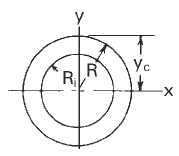 Circular Ring Dimensional Properties |
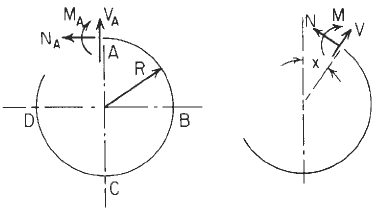 Resultant moment, hoop load, and radial shear |
|
Preview: Circular Ring Moment, Hoop Load, and Radial Shear Calculator
General formulas for moment, hoop load, radial shear and deformations.
Moment
M = MA - NA R ( 1 - u) + VA R z + LTM
Hoop Stress
N = NA u + Va z + LTN
Radial Shear
V = - NA z + VA u + LTv
LTM LTN, and LTV are load terms for several types of load.
Note: Loads beyond 180° not support in load terms equations.
LTM = ( - W R z ) / 2
LTN = ( - W z ) / 2
LTv = ( - W u ) / 2
MA = ( W R k2 ) / π
NA = 0
VA = 0
Ri / t ≥ 10 means thin wall for pressure vessels (per. ASME Pressure Vessel Code)
Hoop Stress Deformation Factor α
α = e / R for thick rings
α = I / AR2 for thin rings
A = π [ R2 - Ri2 ]
Transverse (radial) shear deformation factor β
β = 2F (1 + v) e / R for thick rings
β = FEI / GAR2 for thin rings
k1 = 1 - α + β
k2 = 1 - α
Plastic section modulus
F = Z / I c
Z = Zx = Zy = 1.33R3
Ix = Iy = ( π / 4 ) ( R4 - Ri4)
Deformation in the Horizontal Axis

Deformation in the Vertical Axis
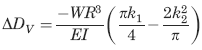
Where (when used in equations and this calculator):
W = load (force);
v and w = unit loads (force per unit of circumferential length);
G = Shear modulus of elasticity
F = Shape factor for the cross section (= Z / I c)
Z = Plastic section modulus
w and v = unit loads (force per unit of circumferential length);
ρ = unit weight of contained liquid (force per unit volume);
Mo = applied couple (force-length);
MA, MB, Mc, and M are internal moments at A;B;C, and x, respectively, positive as shown.
NA N, VA, and V are internal forces, positive as shown.
E = modulus of elasticity (force per unit area);
v = Poisson’s ratio;
A = cross-sectional area (length squared);
R = Outside radius to the centroid of the cross section (length);
Ri = Inside radius to the centroid of the cross section;
t = wall thickness
I = area moment of inertia of ring cross section about the principal axis perpendicular to the plane of the ring (length4). [Note that for a pipe or cylinder, a representative segment of unit axial length may be used by replacing EI by Et3 / 12 (1 - v2 )
e ≈ I / ( R A) positive distance measured radially inward from the centroidal axis of the cross section to the neutral axis of pure bending
θ, x, and Φ are angles (radians) and are limited to the range zero to π for all cases except 18 and 19
s = sin θ
c = cos θ
z = sin x,
u = cos x
n = sin Φ
m = cos Φ
α - Hoop stress deformation factor
ΔDV = Change in vertical diameter (in, mm),
ΔDH = Change in horizontal diameter (in, mm),
ΔL = Change in lower half of vertical diameterthe vertical motion realative to point C of a line connecting points B and D on the ring,
ΔLW = Vertical motion relative to point C of a horizontal line connecting the load points on the ring,
ΔLWH = Change in length of a horizontal line connecting the load points on the ring,
ψ = angular rotation (radians) of the load point in the plane of the ring and is positive in the direction of positive θ.
Reference:
Roarks Formulas for Stress and Strain, 7th Edition