Related Resources: Wheatstone bridge
Wheatstone Bridge Analysis and Calculator
Wheatstone Bridge Analysis and Calculator
In the figure, Rx is the unknown resistance to be measured; R1, R2 and R3 are resistors of known resistance and the resistance of R2 is adjustable. If the ratio of the two resistances in the known leg (R2/R1) is equal to the ratio of the two in the unknown leg (Rx/R3), then the voltage between the two midpoints (B and D) will be zero and no current will flow through the galvanometer eo. If the bridge is unbalanced, the direction of the current indicates whether R2 is too high or too low. R2 is varied until there is no current through the galvanometer, which then reads zero.
Detecting zero current with a galvanometer can be done to extremely high accuracy. Therefore, if R1, R2 and R3 are known to high precision, then Rx can be measured to high precision. Very small changes in Rx disrupt the balance and are readily detected.
At the point of balance, the ratio of
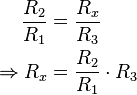
Alternatively, if R1, R2, and R3 are known, but R2 is not adjustable, the voltage difference across or current flow through the meter can be used to calculate the value of Rx, using Kirchhoff's circuit laws (also known as Kirchhoff's rules). This setup is frequently used in strain gauge and resistance thermometer measurements, as it is usually faster to read a voltage level off a meter than to adjust a resistance to zero the voltage.