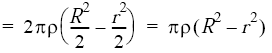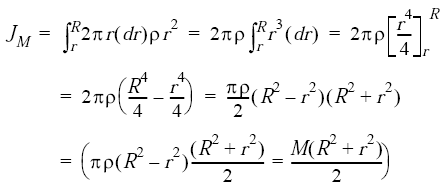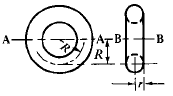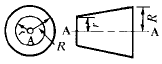Polar Mass Moment of Inertia, Common Shape Equations and Calculator
|
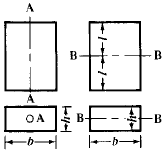
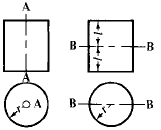
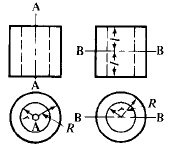
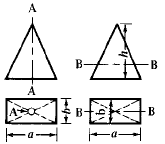
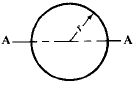
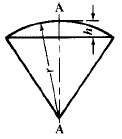
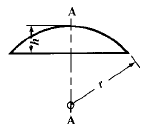
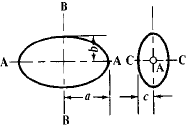
Engineering Metals and Materials Table of Contents Polar Mass Moment of Inertia About Axis A-A, Axis B-B and Axis C-C. Related: Polar Area Moment of Inertia and Section Modulus. Mass Moments of Inertia, JM. formulas for mass moment of inertia of various solids are given below. Example, Polar Mass Moment of Inertia of a Hollow Circular Section: A strip of width dr on a hollow circular section, whose inner radius is r and outer radius is R. The mass of the strip = 2πrdrρ, where ρ is the density of material. In order to get the mass of an individual section, integrate the mass of the strip from r to R.
The 2nd moment of the strip about the AA axis = 2πrdrρr2. To find the polar moment of inertia about the AA axis, integrate the 2nd moment from r to R.
Note: In some many engineering examples the symbol I denotes the polar moment of inertia of masses; JM is used here to avoid confusion with moments of inertia of plane areas. Where: JM = Polar Mass Moment of Inertia (in-lbs-sec2, Kg-m-sec2)
All calculators require a java enabled browser and a Premium Membership Account.
Link to this Webpage: © Copyright 2000 -
2024, by Engineers Edge, LLC |