Related Resources: mechanics machines

Mass Moment of Inertia Equations

Strength & Mechanics of Materials

The mass moment of inertia, usually denoted I, measures the extent to which an object resists rotational acceleration about an axis, and is the rotational analogue to mass. Mass moments of inertia have units of dimension mass × length ². It should not be confused with the second moment of area, which is used in bending calculations.

Geometrically simple objects have moments of inertia that can be expressed mathematically, but it may not be straightforward to symbolically express the moment of inertia of more complex bodies.

Point mass m (mass) at a distance r from the axis of rotation.

I = m R ²

Where:

I = moment of inertia (lb m ft ² , kg m ² )
m = mass (lb m , kg)
R = distance between axis and rotation mass (ft, m)

The moment of all other moments of inertia of an object are calculated from the the sum of the moments.

I = ∑ _i m _i R _i ² = m ₁ R ₁ ² + m ₂ R ₂ ² + ..... + m _n R _n ²

Mass Moment of Inertia

Inertia may be generally expressed as

I = k m R ²

Where:

k = inertial constant
m = mass (lbm , g)
R = distance between axis and rotation mass (in., mm)

General Equation and Calculator Mass Moment of Inertia Calculator

Some Typical Bodies and their Moments of Inertia

Inertia of Cylinder

Thin-walled hollow cylinder:

Moments of Inertia for a thin-walled hollow cylinder is comparable with the point mass and can be expressed as:

I = m R ²

Where:

m = mass of the hollow (lb m , kg)
R = distance between axis and the thin walled hollow (ft, m)

Thin Wall Shaft Mass Moment of Inertia Calculator

Hollow Cylinder (Shaft) Mass Moment of Inertia:

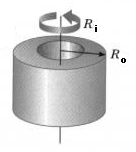
I = 1/2 m ( R _i ² + R _o ² )

Where:

m = mass of hollow (lbm , kg)
R_i = distance between axis and inside hollow (in, mm)
R_o = distance between axis and outside hollow (in, mm)

Hollow Cylinder Shaft Mass Moment of Inertia Calculator

Solid cylinder:

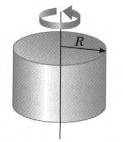
I = 1/2 m R ²

Where:

m = mass of cylinder (lbm , kg)
R = distance between axis and outside cylinder (in, mm)

Solid Shaft Cylinder Mass Moment of Inertia Calculator

Mass Inertia of Sphere

Thin-walled hollow sphere:

I = 2/3 m R ²

Where:

m = mass of sphere hollow (lbm , kg)
R = distance between axis and hollow (in, mm)

Thin Walled Sphere Mass Moment of Inertia Calculator

Solid sphere:

I = 2/5 m R ²

Where:

m = mass of sphere (lbm , kg)
R = radius in sphere (in, mm)

Solid Sphere Cylinder Equation and Calculator Mass Moment of Inertia

Rectangular Plane

Moments of Inertia for a rectangular plane with axis through center:

I = m (a ² + b ² ) / 12

Where:

a, b = short and long sides (in, mm)
m = mass of sphere (lbm , kg)

Rectangular Plane Mass Moment of Inertia Calculator

Moments of Inertia for a rectangular plane with axis along edge:

I = ( m a ² ) / 3

Where:

a = length both sides (in, mm)
m = mass of sphere (lbm , kg)

Rectangular Plate Mass Moment of Inertia Calculator on Edge

Slender Rod

Moments of Inertia for a slender rod with axis through center:

I = ( m L ² )  / 12

Where:

L = length of rod (in., mm)
m = mass of sphere (lbm , kg)

Slender Rod Moment of Inertia Calculator

Moments of Inertia for a slender rod with axis:

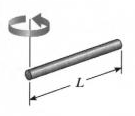
I = 1/3 m L ²

L = length of rod (in., mm)
m = mass of sphere (lbm , kg)

Slender Rod Moment of Inertia Calculator About Edge