Related Resources: material science
Poisson's Ratio Definition Equation
Poisson's ratio is defined as the negative of the ratio of the lateral strain to the axial strain for a uniaxial stress state. If a tensile load is applied to a material, the material will elongate on the axis of the load (perpendicular to the tensile stress plane), as illustrated in Figure 1 (a). Conversely, if the load is compressive, the axial dimension will decrease, as illustrated in Figure 1 (b). If volume is constant, a corresponding lateral contraction or expansion must occur. This lateral change will bear a fixed relationship to the axial strain. The relationship, or ratio, of lateral to axial strain is called Poisson's ratio after the name of its discoverer. It is usually symbolized by v.
Poisson's Ration of Metals and Common Materials
|
Poisson's Ratio Equation:
|
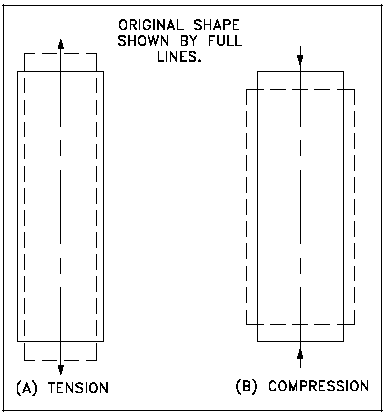 Figure 1
|
Note: Poisson's Ratio has no units
Poisson's ratio is sometimes also reffered to as the ratio of the absolute values of lateral and axial strain. This ratio, like strain, is unitless since both strains are unitless. For stresses within the elastic range, this ratio is approximately constant. For a perfectly isotropic elastic material, Poisson's Ratio is 0.25, but for most materials the value lies in the range of 0.28 to 0.33. Generally for steels, Poisson's ratio will have a value of approximately 0.3. This means that if there is one inch per inch of deformation in the direction that stress is applied, there will be 0.3 inches per inch of deformation perpendicular to the direction that force is applied.
