Pelton Impluse Water Turbine Design Formulas

Related Resources: hydraulic

Pelton Impluse Water Turbine Design Formulas

Pump Engineering and Design
Machine Design and Engineering
Hydraulics and Pneumatics

Pelton Impulse Water Turbine Design Formulas

This is a water turbine in which the pressure energy of the water is converted wholly to kinetic energy in one or more jets which impinge on buckets disposed around the periphery of a wheel. The jet is almost completely reversed in direction by the buckets and a high efficiency is attained. Formulae are given for the optimum pipe size to give maximum power, and for the jet size for maximum power (one jet).

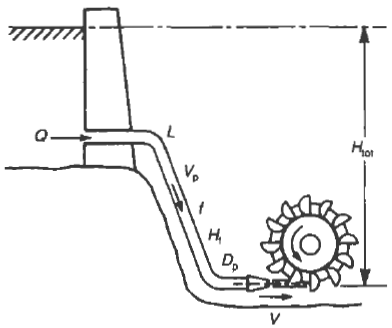
Pelton Wheel with Drop

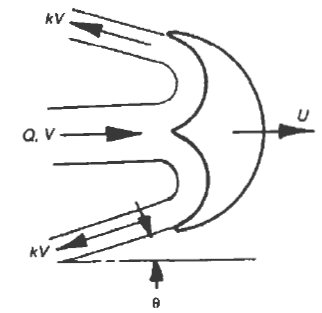
Pelton Water Turbine Forces

Symbols used:
θ = bucket angle
H = available head
H_tot = total head
H_f = friction head
D = mean diameter of bucket wheel
D_p = pipe diameter
d = jet diameter
ρ = water density
g = gravity
f = pipe friction factor
L=length of pipe
η_h = hydraulic efficiency
η_m = maximum efficiency at ( r = 0.5 )
N = wheel speed
C_v =jet velocity coefficient
Q = flow through jet
U = mean bucket speed
V = jet velocity
V_p = pipe velocity
η_o = overall efficiency

Available head H = (H_tot - H_f)
Shaft power P = pgHη_o
Jet velocity V = C_v (2gH)^0.5
Mean bucket speed U = πDN
Flow through jet Q = πd²V/4
Hydraulic efficiency η_h = 2r (1 - r) (1 + k cosθ)
where: r = U/V, θ = bucket angle (4-7°)
k = friction coefficient (about 0.9)

Maximum efficiency (at r = 0.5):
η_m(max) = ( 1 + k cosθ ) / 2

Overall efficiency
η_o = η_hη_m

Maximum power when: H_f = H_tot / 3 = ( 4fLV_p² ) / ( 2gF_p )

Optimum size of supply pipe
D_p = [ ( f L Q² ) / H_tot ] ^1/5 Approximately

Jet size for maximum power d = [ D_p⁵ / ( 8 F L )]^1/4

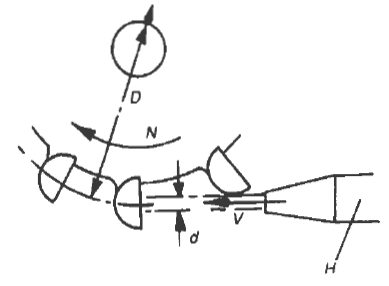
Pelton Turbine Angular Forces and wheel speed

Reference:

Mechanical Engineering Data Book, Butterworth Heinemann, Carvill, James 2003

Link to this Webpage:

Copy Text to clipboard