Related Resources: heatlossinsulatedpipe
Heat Loss Insulated Pipe Equation and Calculator
Equations and calculator to determine the conductive heat loss through a cylinder with multiple layers that may include a pipe wall insulation.
The temperature gradient within a homogeneous material results in an energy transfer rate within the medium which can be calculated with the following equation
![]() eq. a
eq. a
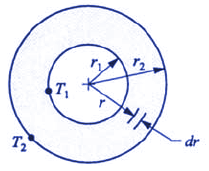
The illustration above depicts a single-layer cylindrical wall of a homogeneous material with constant thermal conductivity and uniform inner and outer surface temperatures. At a given radius the area normal to radial heat flow by conduction is 2 Π r L, where L is the cylinder length. Substituting this into (eq. a) and integrating with q constant gives:
![]() eq. 0
eq. 0
or
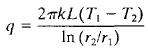 eq. 1
eq. 1

ALL calculators require a Premium Membership
Preview Heat Loss Insulated Pipe Calculator
From (eq 1) the thermal resistance of the single cylindrical layer is [ ln (r2 / r1) ] / 2rkL. For a two-layered cylinder show below the heat transfer rate is,
Conductive Heat Flow = Overall Temperature Difference / Summation of Thermal Resistance's
![]() eq 2
eq 2
or
![]() eq 3
eq 3
Where:
k = thermal conductivity (Btu / h · in· °F)
ka = thermal conductivity inner wall (Btu / h · in· °F)
ka = thermal conductivity outer wall (Btu / h · in · °F)
L = length of cylinder and insulation layer (in)
q = conduction (Btu / h · °F)
The following is the original (pre-7/2016) equations and calculator:

|
|
|
ΔT = (TsEst - Ta) hs = ΔT - Ds + ΔT2 + Ds2 - ΔT Ds |
Related:

