| Fluid Flow Table of Contents
Hydraulic and Pneumatic Knowledge
Fluid Power Equipment
Pipe Friction Calculations Within Pipe For Fluid Flow
Hazen-Williams formula:
where:
hL = head loss, m (ft)
L = length of pipe, m (ft)
Le = equivalent length of pipe for minor losses, m e
(ft)
V = fluid velocity, m/s (ft/s)
a = empirical constant, 0.85 for SI units (1.318 for
IP units)
C = Hazen-Williams coefficient
Di = inside pipe diameter, m (ft)
The Hazen-Williams formula is empirically derived and is limited to use with fluids that have a kinematic viscosity of approximately 1.12 x 10-6 m2 /s (1.22 x 10-5 ft2 /s), which corresponds to water at 15.6 C (60 F), and for turbulent flow. Deviations from these conditions can lead to significant error. The Hazen-Williams coefficient, C, is independent of the Reynolds number. The Pipe Roughness Coefficient Chart provides values of C for various pipe materials.
The Chezy-Manning equation is occasionally applied to full pipe flow. The use of this equation requires turbulent flow and an accurate estimate of the Manning factor, n, which varies by material and increases with increasing pipe size. Pipe Roughness Coefficient Chart provides values of n for various pipe materials. The Chezy-Manning equation is:
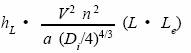
where:
hL = head loss, m (ft)
V = fluid velocity, m/s (ft/s)
n = Manning factor
a = empirical constant, 1.0 for SI units (2.22 for IP units)
© Copyright 2000 - 2009, by Engineers Edge, LLC All rights reserved.
Disclaimer
|
