Application of Bernoulli's Equation to a Venturi
Fluid Flow Table of Contents
Hydraulic and Pneumatic Knowledge
Application of Bernoulli's Equation to a Venturi
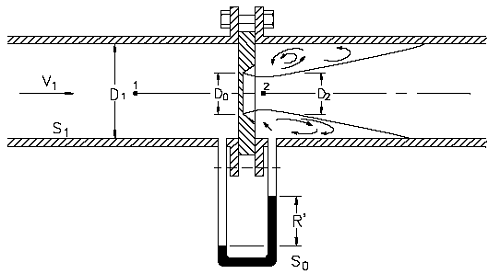
Many plant components, such as a venturi, may be analyzed using Bernoullis equation and the continuity equation. A venturi is a flow measuring device that consists of a gradual contraction followed by a gradual expansion. An example of a venturi is shown in Figure 6. By measuring the differential pressure between the inlet of the venturi (point 1) and the throat of the venturi (point 2), the flow velocity and mass flow rate can be determined based on Bernoullis equation.
Figure 1 Venturi Meter
Bernoullis equation states that the total head of the flow must be constant. Since the elevation does not change significantly, if at all, between points 1 and 2, the elevation head at the two points will be essentially the same and will cancel out of the equation. So Bernoullis equation simplifies to this equation 1 for a venturi.
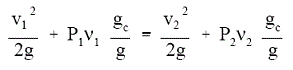
Equation 1
Applying the continuity equation to points 1 and 2 allows us to express the flow velocity at point 1 as a function of the flow velocity at point 2 and the ratio of the two flow areas.
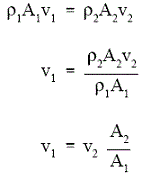
Equation 2
Using algebra to rearrange Equation 1 and substituting the above result for v1 allows us to solve for v2.
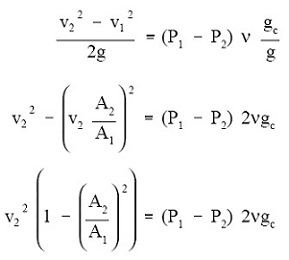
Equation 3
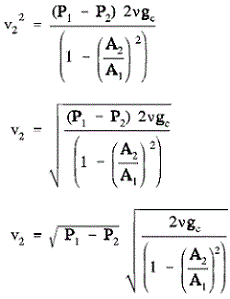
Equation 4
Therefore the flow velocity at the throat of the venturi and the volumetric flow rate are directly proportional to the square root of the differential pressure.
The pressures at the upstream section and throat are actual pressures, and velocities from Bernoullis equation without a loss term are theoretical velocities. When losses are considered in the energy equation, the velocities are actual velocities. First, with the Bernoulli equation (that is, without a head-loss term), the theoretical velocity at the throat is obtained. Then by multiplying this by the venturi factor (Cv), which accounts for friction losses and equals 0.98 for most venturis, the actual velocity is obtained. The actual velocity times the actual area of the throat determines the actual discharge volumetric flow rate.
The pressure drop, P1-P2, across the venturi can be used to measure the flow rate using a U-tube manometer as shown in Figure 1. The reading, R, of the manometer is proportional to the pressure drop and thus the velocity of the fluid.
Related: