| Strength
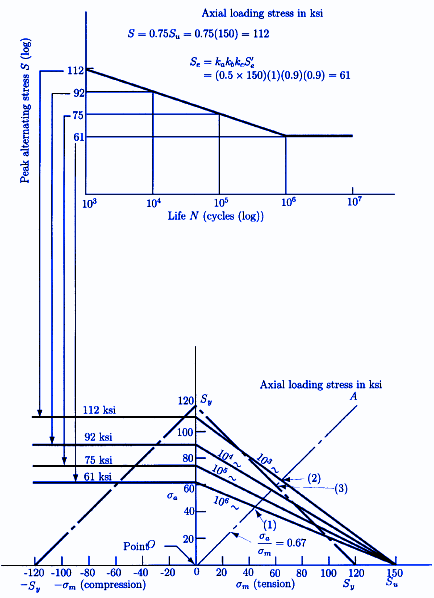
and Mechanics of Materials Randomly Varying Loads Fatigue Life - For the most mechanical parts acted upon by randomly varying stresses, the prediction of fatigue life is not an easy task. The procedure for dealing with this situation is often called the linear cumulative damage rule. The idea is
as follows: If a part is cyclically loaded at a stress level causing failure in 105 cycles, then each cycle of that loading consumes one part in 105 of the life of
the part. If other stress cycles are interposed corresponding to a life of 104 cycles, each of these consumes one part in 104 of the life, and so on. Fatigue
failure is predicted when 100% of the life has been consumed.
Life diagram.
Used with
permission
The linear cumulative damage rule is expressed by:
Where: n1; n2; . . . ; nk represent the number of cycles at speci®c overstress levels and N1; N2; . . . ; Nk represent the life (in cycles) at these overstress
levels, as taken from the appropriate S±N curve. Fatigue failure is predicted when the above equation holds.
Reference: R. C. Juvinall and K. M. Marshek, Fundamentals of Machine Component Design, John Wiley & Sons, New York, 1991.
© Copyright 2000 - 2008, by Engineers Edge, All rights reserved. Disclaimer |
