Related Resources: calculators
Wide Flange with Equal Flanges Intermediate Torque Applied Stress Equations and Calculator
Wide Flange with Equal Flanges Section with Concentrated Intermediate Torque applied Deflection and Stress Equations and Calculator #6 of 1a Loading.
Formulas for the elastic deformations of uniform thin-walled open members under torsional loading.
Per. Roarks Formulas for Stress and Strain - Formulas for torsional properties and stresses in thin-walled open cross sections, Table 10.2.
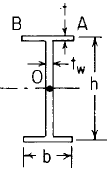
Section Dimensional Definitions Figure 1
Loading Configuration (Section Shown May not Match Section given in Figure 1)
Left end free to twist and warp, right end free to warp but not twist.
Concentrated intermediate torque of Twin Channel With Flanges Inward Beam
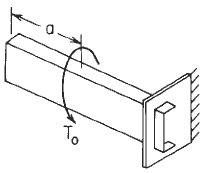
Figure 2
Loading Declarations Image (Section Shown May not Match Section given in Figure 1)
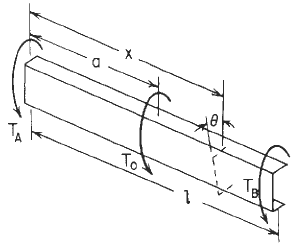
Concentrated intermediate torque of Twin Channel With Flanges Inward Beam Orientation Declarations Image
Figure 3
Preview: W Flange Section Thin wall Stress and Torsional Properties #5 calculator
Twin Channel Section Properties Constants Formulas See: Figure 1
![]()
![]()
Selected maximum values of stress and torsion
![]()
throughout the thickness at points A and B
|
Shear stress due to warping rigidity |
|
throughout the thickness at a point |
|
at the surface everywhere |
Shear stress due to torsional rigidity
![]()
Left end free to twist and warp, right end free to warp but not twist Formulas:
Boundary values for Loading condition See Figure 2
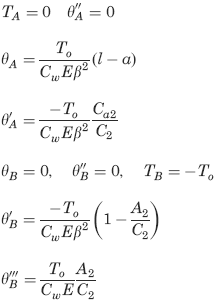
The following constants and functions are hereby defined in order to permit condensing the tabulated formulas which follow.
Concentrated intermediate torque See Figure 3

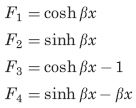
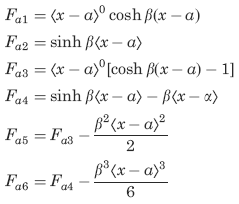
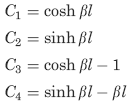
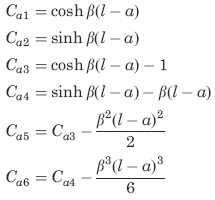
![]()
Where (when used in equations and this calculator):
Point 0 indicates the shear center se "Concentrated intermediate torque of Channel Beam Orientation Declarations image ";
e = distance from a reference to the shear center (in, m);
K = torsional stiffness constant (in4, m4);
C =warping constant (in6, m6);
τ1 = shear stress due to torsional rigidity of the cross section (lbsf/in2, m2);
τ2 = shear stress due to warping rigidity of the cross section (lbsf/in2, m2);
σx = bending stress due to warping rigidity of the cross section (lbsf/in2, m2);
E = modulus of elasticity (lbs/in2, m2);
G = modulus of rigidity (shear modulus) of the material (lbs/in2, m2);
To = applied torsional load (in-lbs, N-m);
to = applied distributed torsional load (lbsf/in, N/m);
TA and TB are the reaction end torques at the left and right ends, respectively (in-lbs, N-m);
θ = angle of rotation at a distance x from the left end (radians).
θ', θ'', θ''', = are the successive derivatives of y with respect to the distance x;
Cw = the warping constant for the cross section;
A, B, C, D, E, F, e, h, b1= Dimensional data Figure 1 (in, m).
All rotations, applied torsional loads, and reaction end torques are positive as shown (CCW when viewed from the right end of the member)
Unit step function defined by use of ⟨ ⟩
⟨ x - θ ⟩0
if x < a, ⟨ x - a ⟩n =0;
if x > a, ( x - a) n ;
The function sinh β
β = ( KG/CwE)1/2
Supplemental selected special cases and maximum values (not included in calculator), See Figure 2.
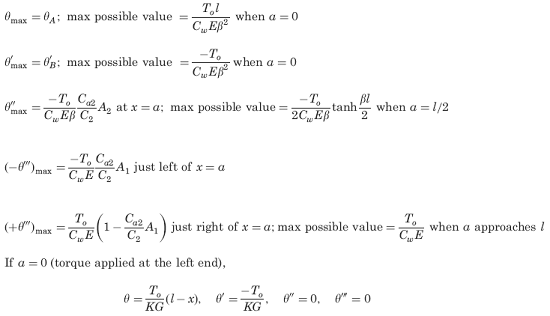
Reference:
Roarks Formulas for Stress and Strain, 7th Edition, Table 10.2 and 10.3 Formulas for torsional properties and stresses in thin-walled open cross sections.