Petroffs Hydrodynamic Lubrication Formula and Calculator

Related Resources: calculators

Petroffs Hydrodynamic Lubrication Formula and Calculator

Fluids Design Engineering
Hydraulic Engineering
Bearing Design and Engineering

Petroff's Hydrodynamic Lubrication Formula and Calculator

Hydrodynamic lubrication is defined when the surfaces of the bearing are separated by a film of lubricant, and does not depend upon the introduction of the lubricant under pressure. The pressure is created by the motion of the moving surface. Hydrostatic lubrication is defined when the lubricant is introduced at a pressure sufficiently high to separate the surfaces of the bearing.

A hydrodynamic bearing (hydrodynamic lubrication) is considered in Fig. 1.0. There is no lubricant flow in the axial direction and the bearing carries a very small load. The radius of the shaft is R, the clearance is c, and the length of the bearing is L (Fig. 1.0). The shaft rotates with the angular speed n rev/s and its surface velocity is V = 2 π R n.

Preview: Petroff's Hydrodynamic Lubrication Calculator

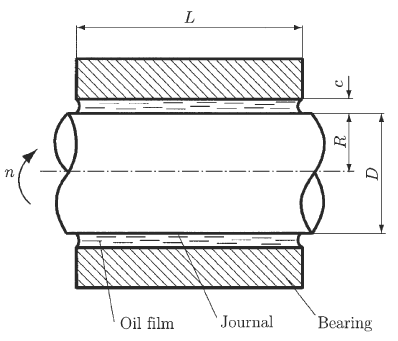
Petroff's Equation Hydrodynamic Lubrication
Figure 1

The shearing stress is:

Eq. 1
τ = µ ( V / s ) = ( 2 π R µ n ) / c

The force required to shear the film is the stress times the area,

Eq. 2
F = τ A,

The torque is the force times the lever arm,

Eq. 3
T = F R = ( τ A ) R

T = [ ( ( 2 π R µ n ) / c ) 2 π R L ] R = ( 4 π² µ n L R³ ) / c

If a small radial load W is applied on the bearing, the pressure P (the radial load per unit of projected bearing area) is

Eq. 4
P = W / ( 2 R L )

The frictional force is fW, where f is the coeffcient of friction, and the frictional torque is

Eq. 4
T_f = - f ( W ) R = f ( 2 R L P ) R = 2 R² f L P

From Eqs. (3) and (4, the coeffcient of friction is

Eq. 5
f = 2 π² ( µ n / P ) ( R / C )

This is called Petroff's law or Petroff's equation. In Petroff's equation there are two important bearing parameters: the dimensionless variable ( µ · n / P ), and the clearance ratio ( R / c ) with the order between 500 and 1000.

The bearing characteristic number, or Sommerfeld number S, is given by

Eq. 6
S = ( µ n / P ) ( R / c )²

where R is the journal radius (in), c is the radial clearance (in), m is the absolute viscosity (reyn), n is the speed ( rev / s ), and P is the pressure (psi). The power loss is calculated with the relation

Eq. 7
H = 2 π T_f n

Declarations

D = shaft diameter, m
R = shaft radius, m
L = bearing length, m
W = force applied, N
c = radial clearance between shaft and bearing, m
n = shaft pevolutions per. minute, rev/min
µ = hydrodynamic fluid viscosity, Pa - s
P = fluid pressure Pa
f = coefficient of friction
T_f = friction torque, N-m
H = power loss, W
S = Sommerfeld number or bearing characteristic number

Credits:

Mechanical Engineers Handbook
Edited by:
Dan B. Marghitu
Department of Mechanical Engineering, Auburn University

Editor
J. David Irwin
Auburn University