Related Resources: calculators
Beam with Single Point and Moment Loading on Elastic Foundation
Beam Deflection and Stress Calculators with Formulas
Beam with Single Point and Moment Loading on Elastic Foundation Calculator and Equations Loading Case 3
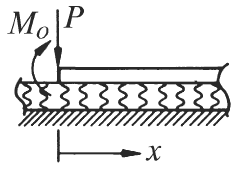
Elastic Beam Loading Single Point and Moment
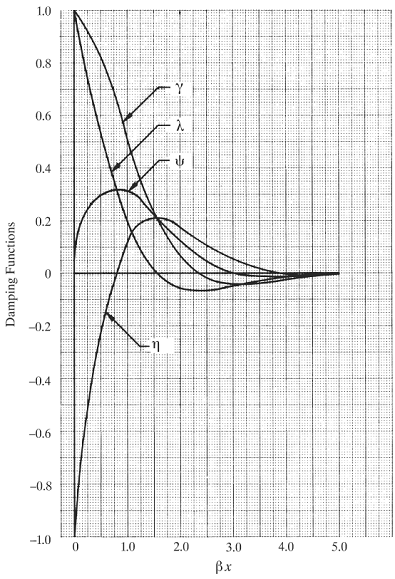
When a beam rests on one or more elastic foundations the final beam deflection and internal shears and bending moment depends on the foundation stiffness as well as the beam stiffness. To make the equation convenient the foundation constant β is available from Figure 1 and the damping functions (γ, λ, ψ, η,) are obtained from Figure 2.
Preview: Beam on Elastic Foundation Calculator and Equations Loading Case 3
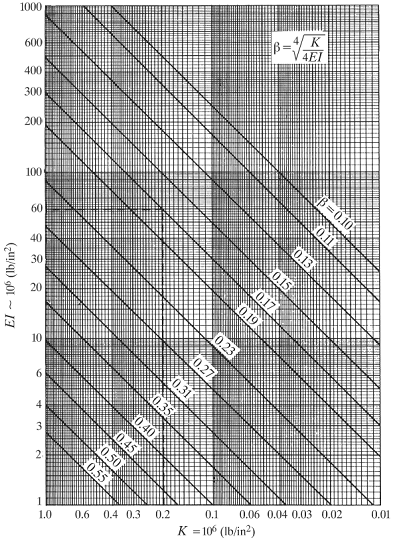
Figure. 1. Foundation Constant β
Eq. 1
M = Mo ( λ ) - P ( ψ ) / β
Eq. 2
V = 2 Mo β ( ψ ) + P ( η )
Eq. 3
y = 2 β [ Mo β ( η ) + P ( λ ) ] / K
Eq. 4
K = p / y
Eq. 5
β = [ K / ( 4 E I ) ] (1/4)
Eq. 6
γ = e-βx ( cos βx + sin βx )
Eq. 7
ψ = e-βx sin βx
Eq. 8
η = e-βx ( sinβx - cosβx )
Eq. 9
λ = e-βx cos βx
Declarations
P = Applied Load (lbs)
p = Load per unit length (lbs / in)
Mo = Moment (in-lbs)
V = Shear (lbs)
E = Modulus of Elasticity (psi)
I = Area moment of inertia (in4)
K = p / y = spring constant of the foundation
p = load per unit length lbs/in
y = deflection (in)
x = distance from applied force (in)
Note: The beam must extend a minimum distance x = 5 / β beyond the applied loads of moments
β = Foundation constant
ψ = damping constant (Figure 2)
η = damping constant (Figure 2)
γ = damping constant (Figure 2)
λ = damping constant (Figure 2)
Related:
- Elastic Foundation Beam With Moment Loading Calculator and Equations Loading Case 2
- Beam on Elastic Foundation Single Point Loading at Center Case 1 Calculator and Equations
- Continuous Plate Supported on an Elastic Foundation Stress and Deflection Equation and Calculator
- Flat Plates Stress, Deflection Equations and Calculators
- Double Integration Method for Beam Deflections
- Reaction and Deflection Case 5M Elastic Frame Roark's Formulas for Stress and Strain Formulas and Calc
- Reaction and Deflection Case 5N Elastic Frame Roark's Formulas for Stress and Strain Formulas and Calc
- Elastic Frame Deflection and Loading Case 5h Formulae and Calculator per. Roark's Formulas for Stress and Strain
Credits:
M. Hete'nyi, - Beams on Elastic Foundation