|
Beam Deflection and Stress Formula and Calculators
Area Moment of Inertia Equations & Calculators
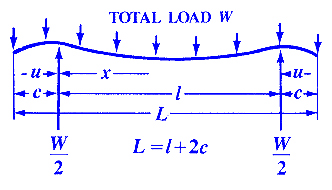
Structural Beam Deflection, Stress, Bending Equations and calculator for a Beam Supported on Both Ends With Overhanging Supports of equal Length and Uniform Loading .
Open
Deflection and Stress Beam For Supported on Both Ends Calculator
Stress between nearest support point and outer end
Stress between the two supports
Stress at load center
Stress at supports
If cross-section is constant,
the greater of these is the
maximum stress.
If l is greater than 2c, the
stress is zero at points on both sides
of the center.
If cross-section is constant
and if l = 2.828c, the stresses
at supports and center are
equal and opposite, and are:
Deflection between support point and outer end
 
Deflection between supports
Deflection at the ends
Deflection at center
If l is between 2c and 2.449c,
there are maximum upward deflections
at points
on
both sides of the center, which are,
Where:
| E = |
Modulus of Elasticity |
psi |
(N/mm2) |
| I = |
Moment of Inertia |
in4 |
(mm4) |
| W = |
Load |
lbs |
(N) |
| s = |
Stress at the cross-section being evaluated |
Lbs/in2 |
(N/mm2) |
| y = |
Deflection |
inches |
(mm) |
| x = |
Some distance as indicated |
inches |
(mm) |
| u = |
Some distance as indicated |
inches |
(mm) |
| c = |
Some distance as indicated |
inches |
(mm) |
| L = |
Some distance as indicated |
inches |
(mm) |
 = |
Some distance as indicated |
inches |
(mm) |
Z = |
section modulus of the cross-section of the beam = I/z |
in3 |
(mm3) |
z = |
distance from neutral axis to extreme fiber (edge) |
inches |
(mm) |
- Please note letter "" (lower case "L") is different than "I" (Moment of Inertia).
- Deflections apply only to constant cross sections along entire length.
References:
- Any Machinery's Handbook published since 1931 or,
- Machinery's Handbook, 21st Edition, Page 405 or,
- Machinery's Handbook, 23st Edition, Page 261 or,
- Machinery's Handbook, 27st Edition, Page 26
|
