Normal or Gaussian Distribution and Reliability Engineering

 There are two principal applications of the normal distribution to engineering and reliability. One application deals with the analysis of items which exhibit failure due to wear, such as mechanical devices. Frequently the wear-out failure distribution is sufficiently close to normal that the use of this distribution for predicting or assessing reliability is valid.

 Another application is in the analysis of manufactured items and their ability to meet specifications. No two parts made to the same specification are exactly alike. The variability of parts leads to a variability in systems composed of those parts. The design must take this part variability into account, otherwise the system may not meet the specification requirement due to the combined effect of part variability. Another aspect of this application is in quality control procedures. The basis for the use of normal distribution in this application is the central limit theorem which states that the sum of a large number of identically distributed random variables, each with finite mean and variance, is normally distributed.

Thus, the variations in value of electronic component parts, for example, due to manufacturing are considered normally distributed.

The failure density function for the normal distribution is:

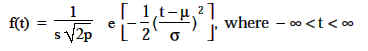
Where:

= The population mean

= Population standard deviation, which is the square root of the variance.

© Copyright 2000 - 2012, by Engineers Edge, LLC All rights reserved.
Disclaimer

Home
Engineering Store
Engineering Training PDH
Products & Services
Engineering Forum
Engineering Design Data
Engineering News
Engineering Videos
Engineering Calculators
Engineering Jobs
Industrial News Buzz
Newsletter Register
Feedback
GD&T Training ASME Y14.5-2009
DFM Training
Contribute Article

Copyright Notice