Related Resources: material science
Shrink Thermal Fit Review
For example a reciprocating engine cylinder walls can become very worn from use. In such cases the use of a sleeve or liner can restore proper fit, form and clearances to the engine cylinder. Sleeves can be made out of steel alloys and are very reliable.
First, the engine block is mounted on a precision boring machine where the worn cylinder is bored to a size much larger than normal and a new allow sleeve is then inserted.
Typically the sleeves cooled down and the engine block heated up to known temperatures then these components are pressed or easily slipped together. When the engine block cools down it shrink fits around the sleeve holding it into place. Once a sleeve has been installed the cylinder needs to be finish bored and honed to obtain the desired precision size and form.
Another common method used in industry is the use of induction shrink fitting which refers to the use of induction heating technology to pre-heat metal components between 150°C and 300°C thereby causing them to expand and allow for the insertion or removal of another component. Other methods of shrink-fitting include compression shrink fitting which uses a cryogen such as liquid nitrogen to cool the insert, while heating the housing.
Calculations For Shrink Fitting
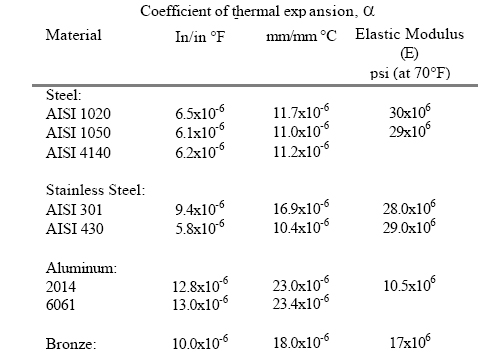
The amount that a particular metal will expand can be calculated using the coefficient of thermal expansion:
d = aL(Dt)
d = Total deformation desired (in or mm)
a = Coefficient of thermal expansion (in/in °F or mm/mm °C)
L = Nominal length of the part being heated (the diameter for a cylinder) (in or mm)
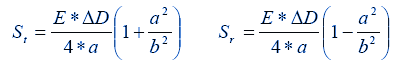
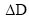 = Change of inner diameter of hole.
= Change of inner diameter of hole.