Hookes Law - Strength (Mechanics) of Materials
Mechanics of Materials Table of Content
Hookes Law - If a metal is lightly stressed, a temporary deformation, presumably permitted by an elastic displacement of the atoms in the space lattice, takes place. Removal of the stress results in a gradual return of the metal to its original shape and dimensions. In 1678 an English scientist named Robert Hooke ran experiments that provided data that showed that in the elastic range of a material, strain is proportional to stress. The elongation of the bar is directly proportional to the tensile force and the length of the bar and inversely proportional to the cross-sectional area and the modulus of elasticity.
Hooke's experimental law may be given by:
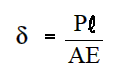
Where:
P = force producing extension of bar (lbf)
l = length of bar (in.)
A = cross-sectional area of bar (in.2)
d = total elongation of bar (in.)
E = elastic constant of the material, called the Modulus of Elasticity, or Young's Modulus (lbf/in.2)
The quantity E, the ratio of the unit stress to the unit strain, is the modulus of elasticity of the material in tension or compression and is often called Young's Modulus.
Tensile stress, or simply stress, was equated to the load per unit area or force applied per cross-sectional area perpendicular to the force measured in pounds force per square inch.
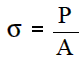
Tensile strain, or the elongation of a bar per unit length, is determined by:
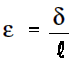
For the equations described above we may adequately expressed by Hooke's Law for elastic materials. For materials under tension, strain (e) is proportional to applied stress s.
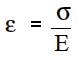
Where:
E = Young's Modulus (lbf/in.2)
s = stress (psi)
e = strain (in./in.)