Related Resources: heat transfer

Heat Loss Insulated Pipe Equation and Calculator

Heat Transfer Engineering
Thermodynamics
Engineering Physics

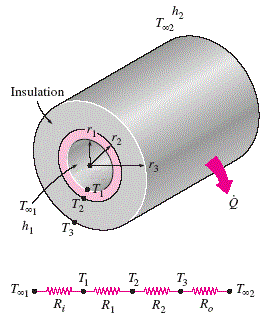
Heat Loss through a Insulated Pipe Equation and Calculator:

Assumptions:

1 Heat transfer is steady since there is no indication of any change with time.
2 Heat transfer is one-dimensional since there is thermal symmetry about the centerline and no variation in the axial direction.
3 Thermal conductivities are constant.
4 The thermal contact resistance at the interface is negligible.

ALL calculators require a Premium Membership

Preview: Heat Loss Through a Insulated Pipe Calculator

Areas of the surfaces exposed to convection:

Individual thermal resistances:

All resistances are in series, the total resistance is:

Steady rate of heat loss:

The heat loss for a given pipe length can be determined by multiplying the above quantity by the pipe length L.

Temperature drops across the pipe and the insulation

Where:

Q = Heat Steady State Transfer (W)
A = Area (m²)
L = Length (m)
r_n = Radius (m)
k = Thermal Conductivity (W/m · °C)
T_∞n = Temperature (°C)
T_n = Temperature (°C)
h_n = Heat Transfer Coefficient (W/m² · °C)
R_{conv, n} = Thermal Resistance (°C/W)
R_insulation1 = Thermal Resistance Glass (°C/W)