|
Heat
Transfer Table of Contents
Heat transfer across a rectangular solid is
the most direct application of Fourier’s law. Heat transfer
across a pipe or heat exchanger tube wall is more complicated
to evaluate. Across a cylindrical
wall, the heat transfer surface area is continually
increasing or decreasing. Figure 3 is
a cross-sectional view of a pipe constructed of a homogeneous
material.
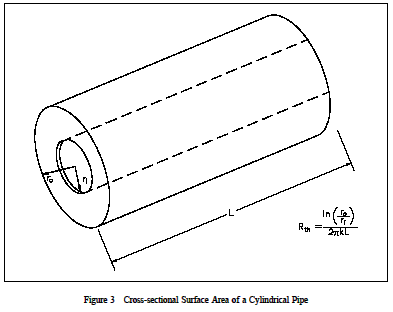
The surface area (A) for transferring heat
through the pipe (neglecting the pipe ends) is directly
proportional to the radius (r)
of the pipe and the length (L) of the pipe.
As the radius increases from the inner wall
to the outer wall, the heat transfer area increases. The
development of an equation evaluating heat transfer through
an object with cylindrical geometry
begins with Fourier’s law Equation 2-5.
From the discussion above, it is seen that no
simple expression for area is accurate. Neither thearea
of the inner surface nor the area of the outer surface alone
can be used in the equation. For a
problem involving cylindrical geometry, it is necessary to
define a log mean cross-sectional area
(Alm).
Substituting the expression 2prL
for area in Equation 2-7 allows the log mean area to becalculated from the inner and
outer radius without first calculating the inner and outer
area.
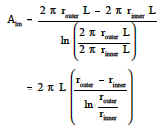(Equation 2-7)
This expression for log mean area can be
inserted into Equation 2-5, allowing us to calculate theheat transfer rate for
cylindrical geometries.
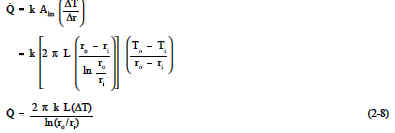
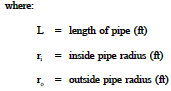
Example:
A stainless steel pipe with a length of 35 ft
has an inner diameter of 0.92 ft and an outer diameter
of 1.08 ft. The temperature of the inner surface of the pipe
is 122oF
and the temperature of
the outer surface is 118oF.
The thermal conductivity of the stainless steel is
108 Btu/hr-ft-oF.
Calculate the
heat transfer rate through the pipe.
Calculate the
heat flux at the outer surface of the pipe.
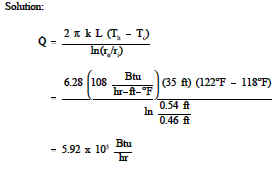
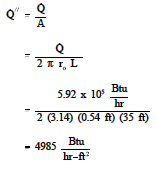
Example:
A 10 ft length of pipe with an inner radius
of 1 in and an outer radius of 1.25 in has an outer
surface temperature of 250°F. The heat transfer rate is
30,000 Btu/hr. Find the interior
surface temperature. Assume k = 25 Btu/hr-ft-°F.
The evaluation of heat transfer through a
cylindrical wall can be extended to include a composite
body composed of several
concentric, cylindrical layers, as shown in Figure 4.
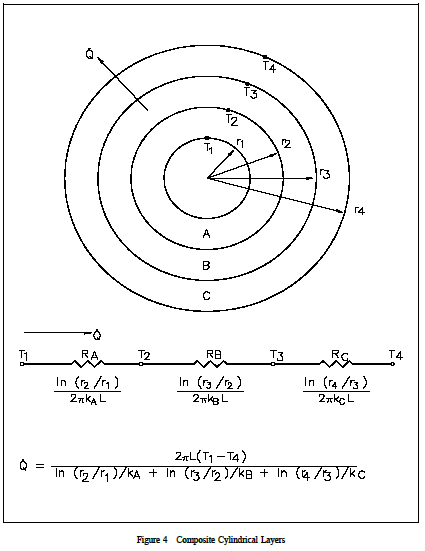
Example:
A thick-walled nuclear coolant pipe (ks
= 12.5 Btu/hr-ft-°F) with 10 in. inside diameter
(ID) and 12 in. outside diameter
(OD) is covered with a 3 in. layer of asbestos insulation
(ka
= 0.14 Btu/hr-ft-oF)
as shown in Figure 5. If the inside wall temperature of the
pipe is maintained at
550°F, calculate the heat loss per foot of length. The
outside temperature is
100°F.
|
