Relationship Between Depth and Pressure Review and Equations
Fluid Flow Table of Contents
Hydraulic and Pneumatic Knowledge
Relationship Between Depth and Pressure Review and Equations
Anyone who dives under the surface of the water notices that the pressure on his eardrums at a depth of even a few feet is noticeably greater than atmospheric pressure. Careful measurements show that the pressure of a liquid is directly proportional to the depth, and for a given depth the liquid exerts the same pressure in all directions.
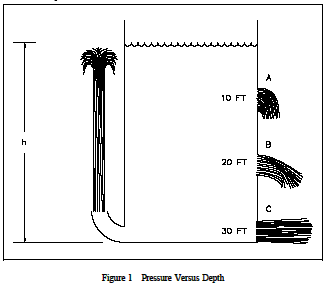
As shown in Figure 1 the pressure at different levels in the tank varies and this causes the fluid to leave the tank at varying velocities. Pressure was defined to be force per unit area. In the case of this tank, the force is due to the weight of the water above the point where the pressure is being determined.
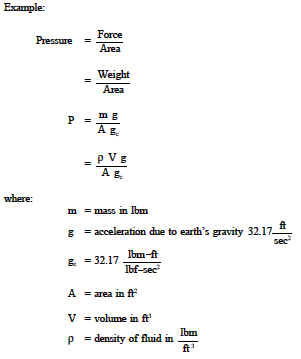
The volume is equal to the cross-sectional area times the height (h) of liquid. Substituting this in to the above equation yields:
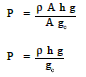
This equation tells us that the pressure exerted by a column of water is directly proportional to the height of the column and the density of the water and is independent of the cross-sectional area of the column. The pressure thirty feet below the surface of a one inch diameter standpipe is the same as the pressure thirty feet below the surface of a large lake.
Example 1:
If the tank in Figure 1 is filled with water that has a density of 62.4 lbm/ft3, calculate the pressures at depths of 10, 20, and 30 feet.
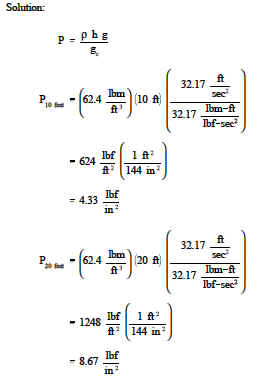

Example 2:
A cylindrical water tank 40 ft high and 20 ft in diameter is filled with water that has a density of 61.9 lbm/ft3.
(a) What is the water pressure on the bottom of the tank?
(b) What is the average force on the bottom?

